Силы инерции второго порядка: Силы инерции второго порядка при уравновешивании четырёхцилиндрового двигателя внутреннего сгорания

Сила — инерция — второе — порядок

Cтраница 1

Сила инерции второго порядка остается неуравновешенной.  [1]

Уравновешивание одноцилиндрового двигателя по методу Ланчестера.  [2]

Сила инерции второго порядка Рщ может быть уравновешена аналогичным методом. Для этого устанавливают еще два вала 03 и С.  [3]

Моменты сил инерции второго порядка при расположении колен, показанном на фиг.  [4]

Уравновешивание сил инерции второго порядка в рассчитываемом двигателе нецелесообразно, ибо применение двухвальной системы с противовесами для уравновешивания 1Рщ значительно усложнит конструкцию двигателя.  [5]

Уравновешивание сил инерции второго порядка в рассчитываемом двигателе нецелесообразно, ибо применение двухвальной системы с противовесами для уравновешивания ЯРщ значительно усложнит конструкцию двигателя.

 [6]

Для уравновешивания сил инерции второго порядка противовесы располагают на шестернях, в два раза меньше по размерам основных, а следовательно, вращающихся в два раза быстрее.  [7]

Для уравновешивания сил инерции второго порядка на дизеле установлен механизм уравновешивания, состоящий из шести противовесов, три из которых размещены в специальном приводе механизма уравновешивания, установленном на заднем торце дизеля, а остальные три находятся в приводе насосов, расположенном на переднем торце дизеля.  [8]

Уравновешивание однорядных многоцилиндровых двигателей. а — четырехцилиндрового. б-шестицилиндрового.  [9]

Суммарная неуравновешенная сила равна учетверенной силе инерции второго порядка одного цилиндра. Равнодействующая этих сил приложена к центру средней коренной шейки и вызывает вибрации двигателя, но эти силы обычно не уравновешивают.

 [10]

Схема расположения.| Схема оппозитного расположения цилиндров.  [11]

Аналогично можно вывести уравнение для сил инерции второго порядка.  [12]

Механизм уравновешивания служит для уравновешивания сил инерции второго порядка движущихся масс кривошипно-шатунного механизма, которые переменны по величине и направлению и действуют в плоскости осей цилиндров.  [13]

Конструктипные схемы механизма уравновешивания.  [14]

Уравновешивающий механизм применяют и в некоторых четырехцилиндровых двигателях для уравновешивания сил инерции второго порядка. Этот механизм установлен на тракторном дизеле А-41 и представляет собой два груза, расположенных на специальных шестернях. Они вращаются в противоположные стороны с частотой, в 2 раза превышающей частоту вращения коленчатого вала.

 [15]

Страницы:      1    2    3    4

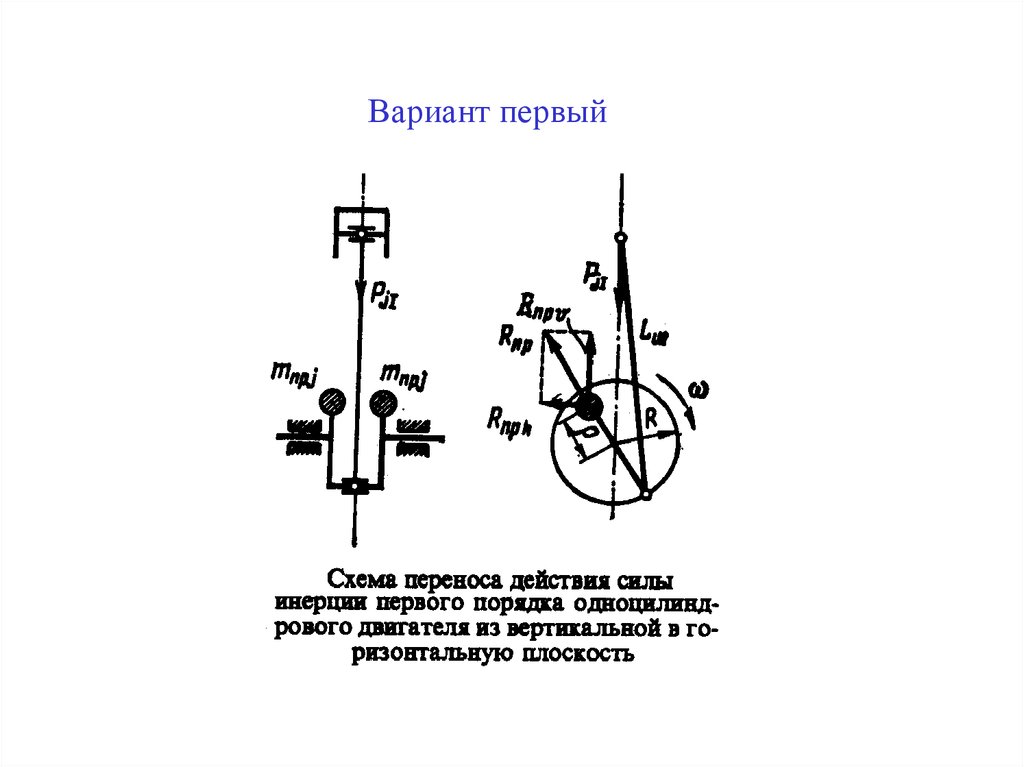
54.Уравновешивание сил инерции 1-го порядка в одноцилиндровом двигателе.

Одноцилиндровый двигатель порождает три вида вибраций (предполагается, что цилиндр расположен вертикально).

Во-первых, без балансирующих противовесов в двигателе будут присутствовать значительные вибрации, порожденные изменением направления движения поршня и шатуна за каждый оборот. Это порождает силу инерции 1-го порядка, которая вызывает вертикальную вибрацию с частотой, равной частоте вращения коленвала. Практически все одноцилиндровые двигатели снабжены балансирующими массами на коленвале для уменьшения этой вибрации.

Хотя эти балансиры устраняют вибрации на коленвале, они не могут полностью сбалансировать движение поршня по двум причинам. Первая причина состоит в том, что балансиры двигаются как по вертикали, так и по горизонтали, поэтому компенсирование вертикального движения поршня массой коленвала порождает горизонтальные вибрации. Массу балансиров подбирают таким образом, чтобы уменьшить вертикальную силу инерции 1-го порядка в два раза, при этом вертикальная и горизонтальная силы инерции становятся равными по величине и, складываясь, образуют круговую силу инерции, вектор которой вращается в сторону, противоположную вращению коленвала. Вторая причина относится к движению шатуна, который из-за конструкции заставляет поршень двигаться в верхней половине цилиндра быстрее, чем в нижней. Это порождает вертикальную силу инерции 2-го порядка, которая вызывает вибрацию с удвоенной частотой вращения коленвала. Поэтому синусоидальное движение коленвала не может полностью скомпенсировать движение поршня. Полностью круговую силу 1-го порядка можно уравновесить двумя балансирующими валами, которые должны располагаться симметрично по бокам коленвала и вращаться в направлении, противоположном направлению вращения коленвала. Противовесы этих валов должны быть одинаковыми и ориентированы так, чтобы создавать такую же по величине круговую силу инерции, но в противоположном направлении.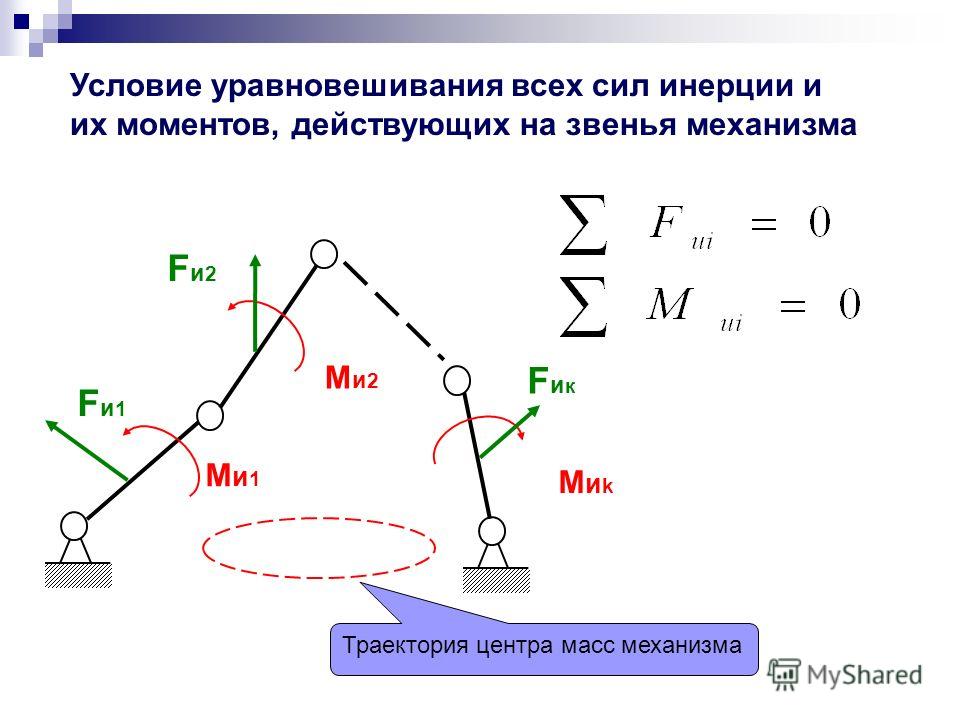

Вертикальную силу инерции 2-го порядка можно уравновесить двумя балансирующими валами, расположенными симметрично по бокам двигателя и вращающимися в противоположные друг относительно друга стороны в два раза быстрее коленвала. Балансирующие массы этих валов также должны быть одинаковыми и ориентированы так, чтобы создавать уравновешивающую вертикальную силу инерции в противоположном направлении. Однако это ведёт к значительному усложнению двигателя, поэтому как правило силу 2-го порядка оставляют неуравновешенной, к тому же она значительно меньше силы инерции 1-го порядка.

Во-вторых, существуют вибрации, порожденные изменением в скорости и кинетической энергии поршня. Так, коленвал будет замедляться, когда поршень ускоряется и поглощает энергию, и будет ускорятся, когда поршень замедляется и отдает энергию в верхней и нижней точке. Эта вибрация имеет удвоенную частоту по сравнению с частотой вращения коленвала, и её поглощение —- задача маховика.

Третий тип вибраций происходит из-за того, что двигатель отдает мощность только во время рабочего хода. В четырехтактном цикле эта вибрация будет на половине частоты

Инерция и масса

Первый закон движения Ньютона гласит, что «Объект в состоянии покоя остается в покое, а объект в движении остается в движении с той же скоростью и в том же направлении, если на него не действует неуравновешенная сила». Объекты склонны «продолжать делать то, что они делают». На самом деле это естественная тенденция объектов сопротивляться изменениям в их состоянии движения. Эта тенденция сопротивляться изменениям в их состоянии движения описывается как инерция

.

Инерция: сопротивление объекта изменению его состояния движения.

 

Представление Ньютона об инерции находилось в прямом противоречии с более популярными представлениями о движении. До Ньютона господствовала мысль, что это естественная склонность объектов останавливаться. Считалось, что движущиеся объекты в конце концов перестанут двигаться; сила была необходима, чтобы держать объект в движении. Но если его предоставить самому себе, движущийся объект в конце концов остановится, а покоящийся объект останется в покое; таким образом, идея, господствовавшая в мышлении людей почти за 2000 лет до Ньютона, заключалась в том, что естественной тенденцией всех объектов является принятие положения покоя.

 

Галилей и концепция инерции

Галилей, выдающийся ученый XVII века, разработал концепцию инерции. Галилей полагал, что движущиеся объекты в конце концов останавливаются из-за силы, называемой трением. В экспериментах с использованием пары наклонных плоскостей, обращенных друг к другу, Галилей заметил, что мяч будет катиться по одной плоскости и подниматься по противоположной плоскости примерно на одинаковую высоту. Если бы использовались более гладкие плоскости, мяч катился бы по противоположной плоскости еще ближе к исходной высоте.

Галилей рассудил, что любая разница между начальной и конечной высотой связана с наличием трения. Галилей постулировал, что если бы трение можно было полностью устранить, то мяч достиг бы точно такой же высоты.

Далее Галилей заметил, что независимо от угла, под которым были ориентированы плоскости, конечная высота почти всегда равнялась начальной высоте. Если бы наклон противоположного склона был уменьшен, то мяч откатился бы на большее расстояние, чтобы достичь первоначальной высоты.

 

Рассуждения Галилея продолжились: если противоположный наклон поднять почти под углом 0 градусов, то мяч будет катиться почти вечно, пытаясь достичь первоначальной высоты. А если бы встречный наклон был даже вовсе не наклонен (то есть если бы он был ориентирован по горизонтали), то… движущийся предмет продолжал бы двигаться… .

 

Смотри! В этом видео объясняется еще один мысленный эксперимент Галилея с использованием реального эксперимента, проведенного с современным оборудованием.

 

​

Силы не заставляют объекты двигаться

Исаак Ньютон основывался на размышлениях Галилея о движении. Первый закон движения Ньютона гласит, что сила равна , а не , необходимой для удержания объекта в движении. Сдвиньте книгу по столу и наблюдайте, как она скользит в исходное положение. Книга, движущаяся по столешнице, не останавливается из-за отсутствие силы; скорее это присутствие силы — эта сила является силой трения — которая приводит книгу в состояние покоя. В отсутствие силы трения книга продолжала бы двигаться с той же скоростью и направлением — вечно! (Или, по крайней мере, до конца столешницы.) Не требуется силы, чтобы удерживать движущуюся книгу в движении. На самом деле это сила, которая останавливает книгу.

 

 

Масса как мера количества инерции

Все объекты сопротивляются изменениям в состоянии их движения. У всех объектов есть эта тенденция — у них есть инерция. Но имеют ли одни объекты большую склонность сопротивляться изменениям, чем другие? Абсолютно да! Тенденция объекта сопротивляться изменениям в его состоянии движения зависит от массы. Масса есть та величина, которая зависит исключительно от инерции объекта. Чем больше инерция у объекта, тем больше у него масса. Более массивный объект имеет большую тенденцию сопротивляться изменениям в своем состоянии движения.

Предположим, что на столе для лекций по физике покоятся два, казалось бы, одинаковых кирпича. Тем не менее, один кирпич состоит из раствора, а другой кирпич состоит из пенополистирола. Не поднимая кирпичи, как вы можете сказать, какой кирпич был кирпичом из пенополистирола ? Вы можете одинаково толкнуть кирпичи, чтобы изменить их состояние движения. Кирпич с наименьшим сопротивлением — это кирпич с наименьшей инерцией — и, следовательно, кирпич с наименьшей массой (т.0054 Пенополистироловый кирпич ).

Обычная физическая демонстрация основана на следующем принципе: чем массивнее объект, тем больше этот объект сопротивляется изменениям в состоянии своего движения. Демонстрация проходит следующим образом: на голову учителя кладут несколько массивных книг. На книги кладут деревянную доску и молотком вбивают в нее гвоздь. Из-за большой массы книг сила удара молота достаточно сопротивляется (инерция). Об этом свидетельствует тот факт, что учитель не чувствует удара молотка. (Конечно, эта история может объяснить многие наблюдения, которые вы ранее делали относительно своего «странного учителя физики».) Обычный вариант этой демонстрации включает разбивание кирпича о руку учителя быстрым ударом молотка. Массивные кирпичи противостоят силе и рука не поранится. (ВНИМАНИЕ: не пытайтесь проводить эти демонстрации дома

 

Смотри! Преподаватель физики объясняет свойство инерции, используя демонстрацию физики phun.

Проверьте свое понимание

1. Представьте себе место в космосе вдали от всех гравитационных и фрикционных влияний. Предположим, вы посещаете это место (только предположим) и бросаете камень. Рок будет

а. постепенно останавливаться.

б. продолжать движение в том же направлении с постоянной скоростью.

2. Объект массой 2 кг движется горизонтально со скоростью 4 м/с. Какая результирующая сила требуется, чтобы тело двигалось с этой скоростью и в этом направлении?

 

3. Мак и Тош спорят в столовой. Мак говорит, что если он бросит желе с большей скоростью, у него будет большая инерция. Тош утверждает, что инерция зависит не от скорости, а от массы. С кем ты согласен? Объяснить, почему.

 

4. Предположим, вы находитесь в космосе в невесомой среде , потребуется ли сила, чтобы привести объект в движение?

 

5. Фред большую часть воскресенья после обеда отдыхает на диване, смотрит профессиональные футбольные матчи и поглощает большое количество еды. Какое влияние (если таковое имеется) оказывает эта практика на его инерцию? Объяснять.

 

6. Бена Туклоуза преследует по лесу лось, которого он пытался сфотографировать. Огромная масса бычьего лося чрезвычайно устрашает. Тем не менее, если Бен сделает зигзагообразный рисунок через лес, он сможет использовать большую массу лося в своих интересах. Объясните это с точки зрения инерции и первого закона движения Ньютона.

 

7. Два кирпича лежат на краю лабораторного стола. Ширли Шешорт встает на цыпочки и замечает два кирпича. У нее появляется сильное желание узнать, какой из двух кирпичей самый массивный. Поскольку у Ширли проблемы с вертикальным положением, она не может дотянуться достаточно высоко и поднять кирпичи; однако она может дотянуться достаточно высоко, чтобы толкнуть кирпичи. Обсудите, как процесс толкания кирпичей позволит Ширли определить, какой из двух кирпичей самый массивный. Какую разницу заметит Ширли и как это наблюдение может привести к необходимому заключению?

 

Следующий раздел:

Перейти к следующему уроку:

Динамические системы второго порядка | Robot Academy

Мы собираемся сделать небольшой обзор простых динамических систем и начнем с очень классической системы, которая представляет собой массу на колесах, соединенную пружиной с фиксированной точкой.

Перемещение тележки относительно некоторых данных задается переменной X. Причем X увеличивается положительно вправо. Если пружина сжата, то она будет толкать тележку влево. А направление указано стрелкой и символом Fs.

Это сила пружины. Теперь мы можем представить себе ситуацию, когда эта пружина растянута, и это случай, когда X отрицательно. И теперь пружина пытается тянуть тележку вправо. Итак, стрелка, указывающая направление Fs, теперь указывает вправо. Таким образом, пружина может либо толкать, либо тянуть тележку, а сила пружины равна минус K, умноженная на X, как я нарисовал эту конкретную диаграмму.

Теперь действует трение, а трение — это сила, противодействующая направлению движения. Итак, на верхнем рисунке, если тележка движется влево, то сила трения будет направлена ​​вправо, и наоборот для рисунка ниже. А сила трения пропорциональна скорости, пропорциональна ẋ А В — коэффициент трения.

Чтобы понять это, мы нарисуем диаграмму свободного тела. Итак, у меня есть масса М и ее перемещение Х. И на массу действовали две силы. Есть сила пружины Kx и сила трения Bẋ.

Ускорение тела равно сумме действующих на него сил. И я могу преобразовать это выражение в эту форму здесь. Итак, это линейное дифференциальное уравнение второго порядка, описывающее движение массы M.

Теперь, если вы немного заржавели в решении дифференциального уравнения, позвольте дать вам подсказку. Мы можем предположить, что X равно E для ST. Что это экспоненциальная функция времени. А S — постоянная времени.

Теперь я мог взять производную от этого и получил выражение для ẋ. И с некоторым упрощением я вижу, что ẋ. равно S, умноженному на X. И я могу снова взять производную и получить вот это выражение. Теперь я могу сделать эти замены в своем исходном уравнении, и я получаю это выражение, и я могу сократить X, и я получаю это, которое называется характеристическим уравнением. Теперь это квадратное уравнение относительно переменной S. И мы можем довольно легко решить его для S.

Вот снова квадратное уравнение, а здесь известное решение квадратного уравнения. Эти значения S известны как полюса системы. И они определяют отклик, отклик положения массы как функцию времени. И помните, что X является экспоненциальной функцией времени и S.

Если мы рассмотрим определитель этого уравнения, это выражение внутри квадратного корня. Он имеет три интересных набора значений. Если определитель больше нуля, то S имеет два действительных и различных значения. Если определитель равен нулю, то S имеет два действительных и равных значения. Два значения S одинаковы. А если определитель меньше нуля, то S — комплексно-сопряженная пара.

С точки зрения физического отклика системы этот случай называется затухающим откликом. Этот случай называется критически затухающим. И этот случай представляет собой колебательный ответ. Общий отклик, положение нашей массы как функции времени — это суперпозиция отклика каждого полюса. Таким образом, это некоторая константа, умноженная на реакцию первого полюса, плюс некоторая константа, умноженная на реакцию из-за второго полюса.

Очень классический способ рассмотрения отклика динамической системы второго порядка, которую мы здесь изучаем, состоит в том, чтобы посмотреть на ее коэффициент демпфирования, который дается приведенным здесь выражением. На графике показана временная характеристика для различных значений коэффициента демпфирования. Когда коэффициент демпфирования больше единицы, мы говорим, что отклик передемпфирован. Мы видим, что он очень медленно реагирует как функция времени. Когда коэффициент демпфирования меньше единицы, мы видим, что отклик несколько колеблется. И по мере того, как коэффициент демпфирования становится все меньше и меньше, мы видим, что отклик системы становится все более и более колебательным. Перебег выше и больше циклов колебаний.

Когда коэффициент демпфирования становится равным нулю, никакого затухания не происходит. И система будет вечно колебаться без какого-либо распада. Коэффициент демпфирования 1 соответствует критическому демпфированию. Это наименьшее значение коэффициента демпфирования, при котором не будет выброса.

Предположим, что теперь мы хотим смоделировать реакцию этого дифференциального уравнения. Я могу переставить его так, чтобы ẍ была изолирована сама по себе с левой стороны. А теперь я собираюсь начать рисовать блок-схему системы, которая имеет ту же динамику, что и наше дифференциальное уравнение. Я собираюсь нарисовать стрелку и обозначить ее ẍ. И я собираюсь добавить интегратор, который мы интегрируем ẍ. И теперь у меня есть ẋ. И я собираюсь снова интегрировать его, и теперь у меня есть X. Сигнал ẋ и умножить его на минус b, тогда я вычислил этот член здесь. А треугольник указывает на блок усиления. Его выход равен минус b, умноженный на его вход.

Затем мы вводим здесь еще один блок усиления с коэффициентом усиления минус K. Если я сложу эти два сигнала вместе с суммирующим соединением, результатом будет выражение, показанное здесь желтым цветом. И если я разделю это на M, то есть применив усиление, равное 1, к M, я вычислю выражение, эквивалентное ẍ.

Итак, я присоединил выход этого блока усиления к сигналу, с которого начал. Итак, это блок-схема динамической системы. И если я создам это в среде моделирования и смоделирую, как это работает в зависимости от времени, сигнал X даст мне реакцию положения динамической системы, которую мы рассматривали в первую очередь. Система с тележкой и пружиной и некоторым трением.

Ну, это система, которую я только что описал, но я реализовал ее в пакете моделирования Simulink, который является частью MATLAB. Вот два интегратора; интегратор, который интегрирует ẍ в ẋ, то есть ускорение в скорость, и этот интегратор, который интегрирует скорость в положение.

Этот конкретный интегратор имеет начальное условие 1. Это начальное значение смещения X. Это начальное положение тележки. То, как мы определяем наши соглашения о координатах, означает, что при X=1 пружина сжимается. Это означает, что первое, что сделает пружина, это оттолкнет тележку. Он будет толкать тележку в направлении -X.

Итак, давайте смоделируем модель, которая у нас есть. А здесь мы видим реакцию тележки на позицию. Как я только что сказал, тележка движется в направлении -X. Он немного колеблется, но энергия уходит из системы, и она останавливается в положении X=0.

Теперь я собираюсь настроить некоторые параметры. Этот блок усиления здесь представляет обратную массу, поэтому я могу открыть здесь настройки параметров и изменить массу с 2 кг на 4 кг. И я собираюсь применить этот параметр. А теперь я собираюсь смоделировать реакцию. Вы заметите, что он меняется. Мы увидим, что колебания на самом деле более интенсивны. И это потому, что наша система начинается с большего количества потенциальной энергии. Это энергия, запасенная в этой сжатой пружине.

Чем больше масса, тем больше начальная потенциальная энергия, которая рассеивается трением дольше. Если я увеличу массу еще больше, увеличу ее до 2 кг, применю это, и здесь мы увидим, что колебания стали намного медленнее, а также скорость затухания намного меньше.

Сейчас я собираюсь вернуть это значение, с которого я начал, которое было 2 кг, смоделировать исходную систему, которая выглядит так. А теперь я собираюсь увеличить количество трения.

Итак, первоначально у нас был коэффициент трения, равный 2, и мы изменили коэффициент трения на 4, и мы должны увидеть, что колебание должно затухать быстрее, потому что энергия рассеивается намного быстрее из-за повышенного трения; увеличьте его еще немного, увеличьте, скажем, до 8, примените этот параметр и снова смоделируйте, и вот мы видим. Сейчас абсолютно никаких колебаний. Система чрезмерно задемпфирована.

Итак, давайте вспомним, как мы преобразуем дифференциальное уравнение в алгебраическое уравнение. Я делаю эти замены для X и его производных ẋ и ẍ в терминах S и X. Теперь возможно, что мы можем рассматривать S как оператор. То есть это оператор, который преобразует дифференциальное уравнение в алгебраическое уравнение. Как только мы это сделали, мы можем найти S, и мы называем эти значения S полюсами этой системы. И они показывают динамическую реакцию системы как функцию времени. Если система имеет более одного полюса, система, которую мы рассматривали, имеет два полюса, то отклик является суперпозицией, суммой отклика, обусловленного каждым конкретным значением S.  

То, что мы рассматривали ранее, называлось непринужденной реакцией. На систему не действовала никакая другая сила, кроме пружины и трения. Ставим тележку на некоторое начальное значение X, не равное нулю. А потом отпустить и смотреть, что происходит.

Теперь меня интересует так называемый принудительный ответ. Теперь я приложу к тележке силу F и хочу понять, как она движется. Итак, я снова рисую диаграмму свободного тела, но теперь она имеет дополнительную силу. У него есть сила, которую я прикладываю к тележке F, а также сила пружины и сила трения. Теперь я рассматриваю баланс сил, действующих на массу на диаграмме свободного тела, и перестраиваю его следующим образом. Теперь я собираюсь рассматривать S как оператор. Я заменяю производные от X оператором S и сейчас напишу это. И вы заметите несколько отличий.

Во-первых, производные исчезли, и я ввел свой оператор S. Вы также заметите, что я заменил строчную букву x на заглавную X и строчную букву f на заглавную F. Что я Я сделал вычисление преобразования Лапласа моего дифференциального уравнения. Заглавная X представляет собой преобразование Лапласа положения тележки в нижнем регистре x, а заглавная F представляет собой преобразование Лапласа приложенной силы, которая является строчной буквой f.

Теперь я могу преобразовать выражение преобразования Лапласа в отношение, которое мы называем передаточной функцией. Это отношение выхода системы X к входу системы F. И для большей ясности я сказал, что капитал X — это функция оператора S, а капитал F — функция оператора S.

Давайте рассмотрим очень общую динамическую систему как черный ящик. На вход подается сигнал x, который является функцией времени, а на выходе сигнал y, который является функцией времени. Тогда математически выход системы y связан с входом в систему x, свернутым с импульсной характеристикой этой динамической системы, которая обозначается G как функция времени.

В области Лапласа, где мы только что работали, все немного проще.