4D это: Что такое четырёхмерное пространство («4D»)? — все самое интересное на ПостНауке

Обычно разработка 4D-модели проводится во время проектирования. Однако эта технология иногда применяется для визуализации непосредственного процесса строительных работ.

Моделирование в формате 4D особенно актуально в случае наличия каких-либо ограничений во время строительства. Ограничения могут быть пространственными (например, стеснённые условия строительства в плотной исторической застройке и т.д.), либо временными – время работ сильно сжато.

Визуально 4D-модель — это подробная анимация процесса строительства. В ней учитывается используемая строительная техника, различные механизмы, места хранения материалов, пути движения техники и рабочих по стройплощадке и т.п.

Основой такой 4D-анимации является 3D-модель, которая возникает по заранее созданному календарному графику проведения работ из последовательно появляющихся элементов. В процессе такой анимации возможны визуальные 4D-коллизии: расположение различных механизмов в одно и то же время в одной точке (наложение), или появление некоторых элементов модели на своих местах раньше, чем это возможно технологически (например, монтаж перекрытия второго этажа до завершения монтажа несущих конструкций первого).

Особенности подготовки данных для 4D моделирования

График проведения работ, линейный или сетевой, подготавливается специалистом заранее, так как программа моделирования сама его составить не может. Сейчас в мире есть задача автоматизировать данный процесс. Например, с помощью технологий искусственного интеллекта (https://www.alicetechnologies.com/). Но такие продукты довольно дороги и поэтому имеют мало примеров реализации (хотя мы активно следим за их развитием). Таким образом, достаточно подробный и грамотно разработанный график строительства обеспечивает качественное моделирование и далее – качественный менеджмент в процессе строительства объекта.

календарный график проектировщиков

В каких программах разрабатывают 4D-модели?

Моделирование строительства может быть реализовано через различные программные продукты. Вот основные из них:

• Autodesk Navisworks
• Synchro Pro
• Bexel Manager

Самый простой вариант – Autodesk Navisworks, где на основе модели из Revit, например, можно сформировать 4D-модель строительства объекта, разделив все элементы на группы, соответствующие позициям в календарном плане строительства.

Такая наглядность может быть оценена, в первую очередь, топ-менеджерами и специалистами заказчика. В большинстве случаев этого бывает достаточно для достижения целей 4D-моделирования. Однако, в случае крупных и сложных проектов может быть недостаточно. В таком случае применяют более сложный инструмент — например, Synchro Pro. В этом программном комплексе созданную в разных BIM-программах модель можно совместить с графиком работ из MS Project или Oracle Primavera. Дополнить полученную анимацию планом стройплощадки с местами движения строительной техники, и создать более качественный и профессиональный прогноз процесса строительства.

Программа BEXEL Manager имеет схожий функционал с перечисленным ПО и также позволяет реализовать 4D моделирование объекта.

После начала строительства 4D-модель позволит визуализировать планируемое и фактическое выполнение работ. Наглядно представлять разницу. В том числе и для тех, кто не очень погружён в процесс строительства (представители заказчика, или, например, покупатели квартир, если речь о жилом многоквартирном доме). Также некоторые программы для 4D-моделирования позволяют идти дальше и заполнять значения ресурсов, необходимых для создания отдельных элементов модели (то есть их стоимость). Для этого типа моделирования уже прижилось понятие 5D, где под пятым «измерением» подразумевают стоимость.

Примеры 4D-визуализации

Наши работы

BIM технологии в проектировании

смотреть

Проектирование торговых центров

смотреть

Проектирование мед.

смотреть

Проектирование пром. зданий

смотреть

BIM проектирование

смотреть

Что такое четырехмерное пространство? — Hi-News.ru

Представление мира в различных измерениях меняет то, как мы воспринимаем все вокруг, включая время и пространство. Думать о разнице между двумя измерениями и тремя измерениями легко, но что насчет четвертого? Важно понимать, что имеют в виду ученые и другие исследователи, когда говорят о различных измерениях: наш мир имеет три пространственных измерения: ширину, глубину и высоту, а четвертым измерением может быть время. Ученые много лет проводят исследования в попытках выяснить что же такое четвертое пространственное измерение, однако по причине того, что наблюдать четвертое измерение мы не можем, доказательства его существования найти очень трудно.

Моделирование движения камеры в четырёхмерном пространстве.

Сколько существует измерений?

Чтобы лучше понимать, на что может быть похоже четвертое измерение, давайте поближе посмотрим на то, что именно делает три измерения трехмерными, и, следуя этим идеям, подумаем о том, что такое четвертое измерение. Итак, длина, ширина и высота составляют три измерения наблюдаемого мира. Все три измерения мы можем наблюдать благодаря эмпирическим данным, а также органами чувств – такими как зрение и слух.

Определить положение точек и направления векторов в трехмерном пространстве можно вдоль опорной точки. Проще всего представить себе трехмерное пространство как трехмерный куб с тремя пространственными осями, которые определяют ширину, высоту и длину куба. Оси движутся вперед и назад, вверх и вниз, влево и вправо вместе со временем – измерением, которое мы непосредственно не наблюдаем, но воспринимаем. При сравнении 3D и 4D, учитывая наблюдения трехмерного пространственного мира, четырехмерный куб будет Тессерактом – объектом, который движется в трех измерениях, которые мы и воспринимаем и в четвертом, которое е можем наблюдать.

Четырехмерный куб (тессеракт) выглядит так

Еще больше статей о последних открытиях в области теоретической физики и высоких технологий читайте на нашем канале в Яндекс.Дзен. Там регулярно выходят статьи, которых нет на сайте.

Четырехмерные объекты и тени

Как пишет Sciencing.com, поскольку трехмерные существа отбрасывают тень на двумерную поверхность Куба, это привело исследователей к предположению о том, что четырехмерные объекты отбрасывают трехмерную тень. Вот почему можно наблюдать «тень» в трех пространственных измерениях, даже если непосредственно наблюдать четыре измерения нельзя.

Математик Генри Сегерман из университета штата Оклахома создал и описал свои собственные 4-мерные скульптуры. Точно так же, как трехмерный объект отбрасывает двумерную тень, Сегерман утверждал, что его скульптуры являются трехмерными тенями четвертого измерения. Хотя эти примеры теней не дают прямых способов наблюдения четвертого измерения, они являются хорошим индикатором того, как думать о четвертом измерении.

Фигуры математика Генри Сегермана выглядят так

Математики часто приводят аналогию с муравьем, идущим по листу бумаги, описывая границы восприятия относительно измерений. Муравей, идущий по поверхности бумаги, может воспринимать только два измерения, но это не значит, что третьего измерения не существует. Это просто означает, что муравей может непосредственно видеть только два измерения и выводить третье измерение через рассуждения об этих двух измерениях. Точно так же люди могут размышлять о природе четвертого измерения, не воспринимая его непосредственно.

Вам будет интересно: Мозг строит странные структуры в 11 измерениях

Четырехмерный куб Тессеракт – это один из примеров того, как трехмерный мир, описываемый x, y и z, может расширяться в четвертый. Математики, физики и другие ученые могут представлять векторы в четвертом измерении, используя четырехмерный вектор, который включает в себя другие переменные, такие как w. Геометрия объектов в четвертом измерении более сложна, так как включает в себя 4-многогранники, которые являются четырехмерными фигурами. Эти объекты показывают разницу между 3D и 4D изображениями.

Существует ли жизнь в четвертом измерении?

То, как выглядели бы существа или жизнь в четырех измерениях, занимало ученых и других специалистов на протяжении десятилетий. В рассказе писателя Роберта Хайнлайна 1940 года «Дом который построил Тим» речь шла о постройке здания в форме Тессеракта. Писатель Клифф Пиковер представлял себе четырехмерных существ как «воздушные шары телесного цвета, постоянно меняющиеся в размерах. Эти существа будут казаться вам разрозненными кусками плоти, точно так же, как двумерный мир позволяет вам видеть только поперечные сечения и остатки мира трехмерного.»

Кадр из мультсериала «Футурама», 15 серия 7 сезона. Перед вами герои в 2D

Четырехмерная форма жизни может видеть вас изнутри точно так же, как трехмерное существо может видеть двумерное со всех сторон.

Джон Нортон из Отдела истории и философии науки Питтсбургского университета считает, что можно прийти к пониманию природы четвертого измерения, задавая вопросы о том, что делает одно -, двух — и трехмерные объекты и явления такими, какие они есть, экстраполируя их в четвертое измерение. Существо, живущее в четвертом измерении, может обладать таким «стереовидением», описанным Нортоном, чтобы визуализировать четырехмерные образы, не будучи стесненным тремя измерениями.

Однако точно ответить на вопрос о том, существуют ли 4D существа сегодня не может никто. Я полагаю, что даже концепция 4D-пространства ожесточенно обсуждается в физических лабораториях, хотя некоторые теории, такие как Теория струн и М-теория, используют существование нескольких измерений для объяснения нашей Вселенной. Важно также отметить, что биологически 4d жизнь не может существовать. А что вы думаете по этому поводу? Присоединятйесь к обсуждению этой темы в комментариях, а также с участниками нашего Telegram чата.

ВселеннаяНаука физика

Для отправки комментария вы должны или

Четырехмерная информационная модель строительного объекта, ее задачи и ошибки создания

Алевтина Герман

Автор, инженер-проектировщик

В статье мы разберем, что такое 4D моделирование, для каких целей его действительно стоит использовать, и рассмотрим на примерах, какие распространенные ошибки допускаются при создании информационной модели строительного объекта.

1. Что такое 4D-моделирование
2. Особенности 4D BIM модели
3. Ошибки 4D модели

4D BIM моделирование — это процесс создания 3D моделей в сочетании с информацией о времени, календарными и сетевыми графиками, управлением логистикой и визуализацией строительства. 4D модель — это визуализация процесса строительных работ, поэтому ее также называют строительной информационной моделью (СИМ).

Александр Лапыгин, обозначает цели создания 4D BIM модели следующим образом:

Для создания качественной 4D модели нужно разобраться с целями, для чего она нужна. Ведь строгого определения этого термина нет, и все его понимают по-своему.

Главная ошибка — это делать 4D ради 4D, то есть не определить цель процесса. От цели уже будут ставиться конкретные задачи, что моделировать, как, в каких программных продуктах и с какими допущениями.

Цели создания модели могут быть, например, такими:

• поиск пространственно-временных коллизий на стройплощадке (при стесненных условиях строительства, крайне ограниченных сроках и/или при наличии большого числа подрядчиков и техники), чтобы заранее запланировать все перемещения техники, материалов и конструкций, исключить физически невозможные технологические операции из-за неверной последовательности работ в графике и т. п. Это довольно дорого, требует большой предварительной работы, но используется в некоторых проектах;
• контроль соблюдения графика строительства с визуальной составляющей. Для этого также нужно сохранить связь 3D модели и графика программно, чтобы можно было в процессе строительства на регулярной основе вносить в график фактические данные, и визуализация процесса позволяла видеть отклонения от графика в виде элементов, которые монтируются с отклонением по времени.
• планирование сроков поставки оборудования и конструкций на площадку на основе 4D модели.

Анализ строительства с применением информационной модели строительного объекта позволяет:

• наглядно представить весь процесс строительства и технологии выполнения работ;
• проверить правильность выбранного сценария выполнения работ;
• оптимизировать зоны строительной площадки;
• выявить и устранить на стадии проекта пространственно-временные коллизии;
• автоматизировано разработать план поставки материально-технических ресурсов с привязкой ко времени;
• оценить возможность альтернативных вариантов монтажа конструкций, траекторий передвижений транспортных средств, перемещений рабочих, разделения элементов конструкции на захватки и фронты работ.

Благодаря этим возможностям, планирование в формате 4D BIM сводит к минимуму риски, сроки и затраты, а также улучшает взаимодействие участников строительства в реальном времени.

Переводом модели из 3D (цифровой информационной модели, или ЦИМ) в 4D занимаются инженеры ПОС (проекта организации строительства) и ППР (проект производства работ). 3D модель в процессе перевода в 4D трансформируется в разряды ресурсов: материальные, технические, трудовые, энергетические и ресурс времени. Корректировка, актуализация и ведение СИМ в ходе работы возможны только при сотрудничестве со специалистами на строительной площадке.

Особенности 4D BIM модели

Если исходить из того, что 4D — это 3D + время, то качественная 4D BIM модель — это трёхмерная информационная модель строительного объекта, в которой все элементы или группы элементов программно связаны с календарным графиком планируемого выполнения работ в соответствии со структурой декомпозиции этих работ, принятых на проекте.

Рассмотрим, что это означает на практике.

Элементы сгруппированы по принципу монтажа
Сама по себе 3D модель должна быть предварительно построена с учётом того, что она будет использоваться для связки с календарным графиком. То есть элементы этой модели сгруппированы так, чтобы каждая группа элементов объединяла элементы, являющиеся частью одной конкретной позиции в графике. Должно быть соответствие модели графику. Хороший метод такой привязки — технология AWP, Advanced work packaging. То есть уже при 3D моделировании должны учитываться все особенности технологии монтажа оборудования.

Типовые ошибки: в большинстве моделей группировку делают не по принципу стадии строительства, а по подобию: кирпичи — к группе стены.

Заполнены все параметры для отдела закупок
Для планирования сроков поставки оборудования и материалов на площадку в трёхмерной модели у каждого элемента, представляющего собой поставочную единицу, должны быть корректно заполнены все параметры, важные для отдела закупок. Для оборудования это может быть наименование производителя и модели, для возводимых на месте элементов — материал, цвет, возможно даже поставщик, если он известен заранее, и т. п.

Для крупногабаритного оборудования должно соблюдаться условие соответствия его габаритов в модели реальным размерам, а также понадобится заполнить параметр массы, чтобы можно было проверить соответствие заложенных в модель характеристик грузоподъемных механизмов той массе, которую им предстоит поднимать.

Структура графика повторяет структуру модели
График должен быть разработан с учётом того, что он будет связываться с 3D моделью. То есть его структура должна повторять структуру модели, а степень детализации (число уровней) должна обеспечивать очередность и объем выполнения работ, должно быть дробление с учетом очередности производимых работ.

Если эти условия соблюдены, такую 4D модель можно использовать для всех трёх целей, озвученных выше.

Подпишитесь на рассылку

Раз в неделю будем присылать вам самые интересные материалы

Согласен с обработкой и хранением моих персональных данных

Или присоединяйтесь к нам в соцсетях:

Ошибки 4D модели

Александр Лапыгин, Генеральный директор РОСЭКО-СТРОЙПРОЕКТ делится опытом:

Разберем возможные ошибки, которые могут возникнуть случайно, из-за нечёткого представления целей и задач моделирования, либо непреднамеренно в силу отсутствия подходящего ПО:

1. Нельзя обновить модель в связке с графиком в процессе строительства. Это приводит к необходимости каждый раз создавать 4D модель заново для анализа текущей ситуации на площадке, это очень трудозатратно и как правило эту работу перестают выполнять, модель теряет связь с реальностью.
2. Структура 3D модели не соответствует структуре графика выполнения работ. В таком случае один элемент модели оказывается задействован в нескольких позициях графика, это усложняет анализ модели.

Пример: перекрытие площадью 1000 м² в модели является одним элементом, а по графику в него укладывают бетон в три параллельных (или последовательных, неважно) захватки, одна 500 м², другая 300, третья 200. Получается, что эти позиции графика нельзя привязать каждую к своему элементу, он у них получается общий, и с такой разбивкой не получится корректно рассчитать сроки его монтажа.

3. Модель разрабатывается в отрыве от реального графика выполнения работ и реальных поставочных спецификаций. Это происходит в случае если моделью занимается обособленное подразделение, а рабочий процесс тем временем идёт «по старинке» и его руководители не разбираются в моделировании, его целях, задачах и преимуществах. Такая модель оказывается неверной и от того бесполезной.
4. Слишком детализированная 3D модель. Это создаёт сложности для просмотра из-за требуемой высокой производительности компьютеров, а также на одну строку графика приходится слишком много позиций модели и их сложно контролировать человеку.

Пример: производитель противопожарных датчиков заказал разработку семейств своего оборудования. Их выполнили в высокой детализации, чтобы порадовать заказчика: каждый датчик включает в себя сложной формы геометрию, отверстия под саморезы, красивый логотип производителя, и имеет вес например 5 Мб (из-за этой сложной геометрии, лого и резьбы). Когда 10 таких датчиков попадают в модель коттеджа, это не сказывается на производительности компьютера, так как вес модели пожарной сигнализации будет около 50 Мб (если брать в расчёт только датчики). А вот когда такие датчики ставят в модель торгового центра площадью 100 000м2, вес системы ПС только из-за датчиков будет под 10 Гб, хотя ценность в них — только место расположения, и параметры (марка), то есть 10 Гб пустой информации занимают оперативную память. Вес «кружка с параметрами» позволил бы иметь объём модели ПС в 50 Мб вместо 10 Гб.

Есть рекомендации производителей софта, например, Autodesk, что одна модель не должна весить больше 500 Мб. Можно ориентироваться на этот показатель. Строго детализация не ограничивается, но нужно понимать, какая детальность минимально достаточна, чтобы не делить файлы на десятки и сотни кусочков, которые потом сложно координировать, и в целом это напрасный труд.

5. Слишком детализированный график: руководитель или планировщик не может его проанализировать.

Степень детализации графика тоже зависит от проекта. График строительства завода СПГ точно будет иметь тысячу строк или более, а иногда бывает и 10 000 позиций. На таких проектах для анализа этих графиков нанимают специального планировщика, или даже команду планировщиков, которые всё время работают только с графиком.

А вот если мы строим себе коттедж, вряд ли позиций будет больше 100. Вручную можно контролировать от 100 строк (если меньше — то график недостаточно детален) до 2000 (если это не уникальный проект с отдельной командой планировщиков).

6. Недостаточная степень детализации модели и/или графика — тогда период контроля результатов работ на площадке оказывается сильно короче длительности позиций нижнего уровня в графике.
7. Главная ошибка — повторюсь — непонимание цели моделирования, и отсутствие связи задач моделирования с этой целью. Если просто пытаться сделать всё, на что способно имеющееся ПО, не задумываясь о том как в строительстве будет использоваться результат, есть риск потратить большие ресурсы на моделирование и календарно-сетевое планирование, и никак не повысить эффективность работ. Тогда моделирование превращается в карго-культ, и результат вызывает у всех участников разочарование.

В следующей статье мы расскажем о том, в каких программах строятся четырехмерные модели и какие требования предъявляются к разным этапам.

Что такое четырёхмерное пространство («4D»)? Как легко и понято объяснить, что такое четырехмерное пространство? Понятие прямой в трехмерном пространстве

Мы привыкли к трем измерениям нашей Вселенной — в длину, в ширину и в глубину. Мы можем представить, как выглядели бы в усеченных измерениях — на плоскости в 2D или вдоль линии в 1D — но представить, как выглядели бы вещи при большем числе измерений, довольно трудно (если вообще возможно). Мы просто не можем представить, как что-то движется в направлении, которое как бы не входит в наше понятие о пространстве. Нашей Вселенной присуще четвертое измерение (время), но она также обладает лишь тремя пространственными. Внимание, вопрос:

Каково было бы людям, если бы число измерений в нашем мире менялось, как времена года? Допустим, полгода мы жили бы в трех измерениях, а другие полгода — в четырех.

Представьте, если можете, что имеете возможность двигаться в дополнительном направлении, помимо вверх-вниз, север-юг, запад-восток. Представьте для начала, что вы единственный в мире, кто так может.

Для кого-то в трехмерном мире вы могли бы делать невероятные вещи, которые — во многом — сделали бы вас богоподобным:

• вы могли бы телепортироваться из одного места в другое, исчезая в одном месте и появляясь где-нибудь еще;
• вы могли бы переставлять или удалять чужие внутренние органы, осуществляя хирургию без необходимости вскрывать кому-то тело;
• вы могли бы просто убрать кого-то из трехмерной Вселенной, в которой он живет, поместив его через некоторое время в другое место по вашему желанию.

С точки зрения нашего дополнительного пространственного измерения мы могли бы попасть внутрь двумерного существа и двигать его внутренности, не разрезая его. Мы могли бы перевернуть его, поменять местами лево и право. Могли бы «забрать» его из его вселенной и поместить куда-то еще.

И если бы мы сами, трехмерные существа, решили попасть бы в их двумерную вселенную, мы выглядели бы странно, поскольку местные жители могли бы видеть лишь двумерные нарезки в отдельно взятый момент.

• потом переросли бы в два круга, по мере нашего «снижения» через их вселенную,
• круги росли бы, пока не соединились в овал,
• затем рядом с ними бы появились другие кружочки (пальцы),
• переросли бы в два больших круга (кисти, руки), вместе с овалом,
• потом все слилось бы в одну большую часть наших плеч,
• затем сузилось бы, выросло и растворилось в наших шеях и головах.

В контексте общей теории относительности весьма просто выстроить пространственно-временные рамки, в которых число «больших» (то есть макроскопических) измерений изменялось бы со временем. Вы не только могли располагать большим числом измерений в прошлом, но и в будущем вам вполне может выпасть такой шанс; вы вообще могли бы построить пространство-время, в котором это число будет колебаться, изменяясь в большую и меньшую сторону со временем, снова и снова.

Для начала все круто: у нас может быть Вселенная с четвертым — дополнительным — пространственным измерением.

Итак, это круто, но как это будет выглядеть? Обычно мы не думаем о таком, но четыре фундаментальных взаимодействия — гравитация, электромагнетизм и два ядерных взаимодействия — обладают такими свойствами и силами, поскольку существуют при тех измерениях, которыми располагает наша Вселенная. -15 метра). Если бы вы позволили этим силам «утекать» в другое пространственное измерение, что они могли бы осуществить только если это измерение достигнет достаточно больших размеров, изменились бы законы взаимодействий, управляющие работой этих сил.

В целом эти силы будут иметь больше «пространства» для разбегания, а значит будут быстрее становиться слабее на дистанции, если будет больше измерений. Для ядер это изменение будет не таким уж плохим: размеры ядер будут больше, некоторые ядра изменят свою стабильность, станут радиоактивными или, напротив, от радиоактивности избавятся. Это ладно. Но с электромагнетизмом будет сложнее.

Представьте, что случилось бы, если бы вдруг силы, связывающие электроны с ядрами, стали слабее. Если бы произошло изменение силы этого взаимодействия. Вы не думаете об этом, но на молекулярном уровне единственное, что вас удерживает, это относительно слабые связи между электронами и ядрами. Если вы измените эту силу, вы измените конфигурации всего остального. Ферменты денатурируют, белки изменят форму, лиганды разойдутся; ДНК не будет кодироваться в молекулах, в которых должна.

Другими словами, если электромагнитная сила изменится, поскольку начнет распространяться в крупное четвертое пространственное измерение, которое достигнет размеров ангстрема, тела людей моментально развалятся, и мы умрем.

Но не все потеряно. Есть много моделей — в основном разработанных в рамках теории струн — где эти силы, электромагнитные и ядерные, ограничены тремя измерениями. Только гравитация может проходить через четвертое измерение. Для нас это означает, что если четвертое измерение будет расти в размере (и, следовательно, в последствиях), гравитация будет «кровоточить» в дополнительное измерение. Следовательно, объекты будут испытывать меньшее притяжение, чем то, к которому привыкли мы.

Астероиды, например, — которые сцепились вместе — разлетятся, поскольку их гравитации окажется недостаточно, чтобы удержать камни вместе. Кометы, приближаясь к Солнцу, будут испаряться быстрее и демонстрировать еще более красивые хвосты. Если четвертое измерение вырастет достаточно большим, на Земле сильно уменьшатся гравитационные силы, в результате чего наша планета вырастет больше, особенно вдоль экватора.

Люди, живущие вблизи полюсов, почувствуют себя словно в среде с уменьшенной гравитацией, а люди на экваторе окажутся в опасности улететь в космос. На макроуровне знаменитый закон тяготения Ньютона — закон обратных квадратов — внезапно станет законом обратного куба, сильно уменьшая силу тяжести с расстоянием.

На Земле настали бы времена, когда мы не только получили бы возможность передвигаться «дополнительным» путем через пространстве, когда обзавелись бы не только дополнительным «направлением», помимо вверх-вниз, влево-право и вперед-назад, но и когда свойства гравитации изменились бы в худшую сторону. Мы прыгали бы выше и дальше, но последствия для ныне стабильной Вселенной были бы апокалиптическими.

Многомерные пространства — миф или реальность? Большинству из нас, или, возможно, всем нам невозможно представить мир, состоящий из более чем трех пространственных измерений. Правильно ли утверждение, что такой мир не может существовать? Или просто человеческий разум не способен вообразить дополнительные измерения — измерения, которые могут оказаться такими же реальными, как и другие вещи, которые мы не можем увидеть?

Мы достаточно часто слышим что-нибудь вроде «трехмерное пространство», или «многомерное пространство», или «четырехмерное пространство». Возможно, вы знаете, что мы живем в четырехмерном пространстве-времени. Что это означает и почему это интересно, почему математики и не только математики изучают такие пространства?

Давайте начнем с простого — начнем с одномерного пространства . Представим себе, что у нас есть город, который расположен вдоль дороги, и в этом городе есть только одна улица. Тогда мы можем каждый дом на этой улице закодировать одним числом — у дома есть номер, и этот номер однозначно определяет, какой дом имеется в виду. Люди, которые живут в таком городе, — можно считать, что они живут в таком одномерном пространстве. Жить в одномерном пространстве довольно скучно, и люди обычно живут не в одномерном пространстве.

Например, если мы говорим про города, то можно перейти от одномерного пространства к двумерному. Примером двумерного пространства является плоскость, а если мы продолжим нашу аналогию с городами, то это город, в котором можно расчертить улицы, допустим, перпендикулярно друг другу, как это сделано в Нью-Йорке, в центре Нью-Йорка. Там есть «стрит» и авеню, каждая из которых имеет свой номер, и вы можете задавать местоположение на плоскости, задавать два числа. Опять же, все мы знаем декартову систему координат, знакомую со школы, — каждая точка задается двумя числами. Это пример двумерного пространства .

Но если мы говорим про город типа центра Нью-Йорка, то на самом деле он является трехмерным пространством, потому что вам мало задать, например, конкретный дом, пусть даже вы зададите его пересечением какой-нибудь «стрит» и какой-нибудь авеню, — вам нужно будет задать еще и этаж, на котором находится нужная вам квартира. Это даст вам третье измерение — высоту. У вас получится трехмерное пространство , в котором каждая точка задается тремя числами.

Вопрос: что такое четырехмерное пространство ? Представить его себе не так-то просто, но можно думать о том, что это пространство, в котором каждая точка задается четырьмя числами. На самом деле мы с вами действительно живем в четырехмерном пространстве-времени, потому что события нашей жизни кодируются как раз четырьмя числами — помимо положения в пространстве, есть еще и время. Например, если вы назначаете свидание, то вы можете сделать это так: вы можете указать три числа, которые будут соответствовать точке в пространстве, и обязательно указать время, которое обычно задается в часах, минутах, секундах, но можно было бы закодировать его одним числом. Например, количество секунд, прошедших с определенной даты, — это тоже одно число. Таким образом получается четырехмерное пространство-время.

Представить себе геометрию этого четырехмерного пространства-времени не очень просто. Например, мы с вами привыкли к тому, что в нашем обычном трехмерном пространстве две плоскости могут пересекаться по прямой либо быть параллельными. Но не бывает такого, чтобы две плоскости пересекались в одной точке. Две прямые могут пересечься в одной точке, а на плоскости не могут в трехмерном пространстве. А в четырехмерном пространстве две плоскости могут и чаще всего пересекаются в одной точке. Можно представлять себе, хотя это уже совсем сложно, пространство большей размерности. На самом деле математики, когда работают с пространствами высокой размерности, чаще всего говорят просто: допустим, пятимерное пространство — это пространство, в котором точка задается пятью числами, пятью координатами. Безусловно, математики разработали разные методы, которые позволяют понимать что-то о геометрии такого пространства.

Почему это важно? Зачем понадобились такие пространства? Во-первых, четырехмерное пространство нам важно, потому что оно применяется в физике, потому что мы в нем живем. А зачем нужны пространства более высоких измерений? Давайте представим себе, что мы изучаем какие-то объекты, которые обладают большим количеством параметров. Например, мы изучаем страны, и у каждой страны есть территория, количество населения, внутренний валовой продукт, количество городов, какие-нибудь коэффициенты, индексы, что-нибудь такое. Мы можем представлять себе каждую страну в виде одной точки в каком-то пространстве достаточно высокой размерности. И оказывается, что с математической точки зрения это правильный способ об этом думать.

В частности, переход к геометрии многомерного пространства позволяет анализировать разные сложные объекты, обладающие большим количеством параметров.

Для того чтобы изучать такие объекты, используются методы, разработанные в науке, которая называется линейная алгебра. Несмотря на то, что она алгебра, на самом деле это наука о геометрии многомерных пространств. Конечно, поскольку представить их себе довольно тяжело, математики используют формулы, для того чтобы как раз изучать такие пространства.

Представить себе четырех-, пяти- или шестимерное пространство довольно сложно, но математики не боятся трудностей, и им мало даже стомерных пространств. Математики придумали бесконечномерное пространство — пространство, содержащее бесконечное количество измерений. В качестве примера такого пространства можно привести пространство всех возможных функций, заданных на отрезке или прямой.

Оказывается, что методы, которые были разработаны для конечномерных пространств, во многом переносятся и на случаи чрезвычайно сложных с точки зрения просто попытки их все представить пространств.

У линейной алгебры есть многочисленные приложения не только в математике, но и в самых разных науках, начиная c физики и заканчивая, например, экономикой или политической наукой. В частности, линейная алгебра является основой для многомерной статистики, которая как раз используется для вычленения связей между различными параметрами в каких-то массивах данных. В частности, популярный ныне термин Big Data зачастую связывается с решением задач по обработке данных, которые представляются именно большим количеством точек в пространстве какой-то конечной размерности. Чаще всего такие задачи можно переформулировать и разумно воспринимать именно в геометрических терминах.

Со школьных лет математика разделяется на алгебру и геометрию. Но на самом деле, если мы задумаемся о том, как устроена современная математика, то мы поймем, что те задачи, которые сейчас решаются, в частности, с применением методов линейной алгебры, на самом деле являются очень отдаленным продолжением тех задач, над которыми задумывались многие тысячи лет назад, например Пифагор или Евклид , разрабатывая ту самую школьную геометрию, которая сейчас есть в любом школьном учебнике. Удивительно, что задача по анализу больших данных оказывается в некотором смысле потомком, казалось бы, совсем бессмысленных — по крайней мере с практической точки зрения — упражнений древних греков по рисованию прямых или окружностей на плоскости или мысленному проведению прямых или плоскостей в трехмерном пространстве.

Что такое четырёхмерное пространство («4D»)?

Тессерракт — четырехмерный куб

Всем знакомо сокращение 3D , означающее «трёхмерный» (буква D — от слова dimension — измерение ). Например, выбирая в кинотеатре фильм с пометкой 3D, мы точно знаем: для просмотра придётся надеть специальные очки, но зато картинка будет не плоской, а объёмной. А что такое 4D? Существует ли «четырёхмерное пространство» в реальности? И можно ли выйти в «четвёртое измерение» ?

Чтобы ответить на эти вопросы, начнём с самого простого геометрического объекта — точки. Точка нульмерна. У неё нет ни длины, ни ширины, ни высоты.

Сдвинем теперь точку по прямой на некоторое расстояние. Допустим, что наша точка — остриё карандаша; когда мы её сдвинули, она прочертила отрезок. У отрезка есть длина, и больше никаких измерений: он одномерен. Отрезок «живёт» на прямой; прямая является одномерным пространством.

Тессеракт — четырехмерный куб

Возьмём теперь отрезок и попробуем его сдвинуть так, как раньше точку. Можно представить себе, что наш отрезок — это основание широкой и очень тонкой кисти. Если мы выйдем за пределы прямой и будем двигаться в перпендикулярном направлении, получится прямоугольник. У прямоугольника есть два измерения — ширина и высота. Прямоугольник лежит в некоторой плоскости. Плоскость — это двумерное пространство (2D), на ней можно ввести двумерную систему координат — каждой точке будет соответствовать пара чисел. (Например, декартова система координат на школьной доске или широта и долгота на географической карте.).

Если сдвинуть прямоугольник в направлении, перпендикулярном плоскости, в которой он лежит, получится «кирпичик» (прямоугольный параллелепипед) — трёхмерный объект, у которого есть длина, ширина и высота; он расположен в трёхмерном пространстве, в таком, в каком живём мы с вами. Поэтому мы хорошо представляем себе, как выглядят трёхмерные объекты. Но если бы мы жили в двумерном пространстве — на плоскости, — нам пришлось бы изрядно напрячь воображение, чтобы представить себе, как можно сдвинуть прямоугольник, чтобы он вышел из той плоскости, в которой мы живём.

Тессеракт — четырехмерный куб

Представить себе четырёхмерное пространство для нас также довольно непросто, хотя очень легко описать математически. Трёхмерное пространство — это пространство, в котором положение точки задаётся тремя числами (например, положение самолёта задаётся долготой, широтой и высотой над уровнем моря). В четырёхмерном же пространстве точке соответствует четвёрка чисел-координат. «Четырёхмерный кирпич» получается сдвигом обычного кирпичика вдоль какого-то направления, не лежащего в нашем трёхмерном пространстве; он имеет четыре измерения.

На самом деле мы сталкиваемся с четырёхмерным пространством ежедневно: например, назначая свидание, мы указываем не только место встречи (его можно задать тройкой чисел), но и время (его можно задавать одним числом, например количеством секунд, прошедших с определенной даты). Если посмотреть на настоящий кирпич, у него есть не только длина, ширина и высота, но ещё и протяженность во времени — от момента создания до момента разрушения.

Физик скажет, что мы живём не просто в пространстве, а в пространстве-времени; математик добавит, что оно четырёхмерно. Так что четвёртое измерение ближе, чем кажется.

Представление других измерений

От 2D к 3D

Ранняя попытка объяснить концепцию дополнительных измерений появилась в 1884 году с публикацией романа о плоской земле Эдвина А. Эббота «Флатландия: романтика множества измерений «. Действие в романе разворачивается в плоском мире, называемом «Флатландия», а повествование ведется от лица жителя этого мира — квадрата. Однажды во сне квадрат оказывается в одномерном мире — Лайнландии, жители которой (треугольники и другие двумерные объекты представлены в виде линий) и пытается объяснить правителю этого мира существование 2-го измерения, однако, приходит к выводу о том, что его невозможно заставить выйти за рамки мышления и представления только прямых линий.

Квадрат описывает его мир как плоскость, населенную линиями, кругами, квадратами, треугольниками и пятиугольниками.

Однажды перед квадратом появляется шар, но его суть он не может постичь, так как квадрат в своем мире может видеть только срез сферы, только форму двумерного круга.

Сфера пытается объяснить квадрату устройство трехмерного мира, но квадрат понимает только понятия «вверх/вниз» и «лево/право», он не способен постичь понятия «вперед/назад».

Только после того, как сфера вытащит квадрат из его двумерного мира в свой трехмерный мир, он наконец поймет концепцию трех измерений. С этой новой точки зрения квадрат становится способен видеть формы своих соотечественников.

Квадрат, вооруженный своим новым знанием, начинает осознавать возможность существования четвертого измерения. Также он приходит к мысли, что число пространственных измерений не может быть ограничено. Стремясь убедить сферу в этой возможности, квадрат использует ту же логику, что и сфера, аргументирующая существование трех измерений. Но теперь из них двоих становится «близорукой» сфера, которая не может понять этого и не принимает аргументы и доводы квадрата — так же, как большинство из нас «сфер» сегодня не принимают идею дополнительных измерений.

От 3D к 4D

Нам сложно принять эту идею, потому что, когда мы пытаемся представить даже одно дополнительное пространственное измерение — мы упираемся в кирпичную стену понимания. Похоже, что наш разум не может выйти за эти границы.

Представьте себе, например, что вы находитесь в центре пустой сферы. Расстояние между вами и каждой точкой на поверхности сферы равно. Теперь попробуйте двигаться в направлении, которое позволяет вам отойти от всех точек на поверхности сферы, сохраняя при этом равноудаленность. Вы не сможете этого сделать..

Житель Флатландии столкнулся бы с такой же проблемой, если бы он находился в центре круга. В его двумерном мире он не может находиться в центре круга и двигаться в направлении, которое позволяет ему оставаться равноудаленными каждой точке окружности круга, если только он не перейдет в третье измерение. Увы, у нас нет проводника в четырехмерное пространство как в романе Эббота, чтобы показать нам путь к 4D.

Что такое гиперкуб? Построение тессеракта

Гиперкуб — это обобщающее название куба в производном числе измерений. Всего измерений десять, плюс точка (нулевое измерение).

Соответственно, существует одиннадцать видов гиперкуба. Рассмотрим построение тессеракта — гиперкуба четвертого измерения:

Для начала построим точку А (рис. 1):

После, соединим ее с точкой В. Получим вектор АВ (рис. 2):

Построим вектор, параллельный вектору АВ, и назовем его CD. Соединив начала и концы векторов, получим квадрат ABDC (рис. 3):

Теперь построим еще один квадрат A1B1D1C1, который лежит в параллельной плоскости. Соединив точки подобным образом, получим куб (рис. 4):

У нас есть куб. Представьте, что положение куба в трехмерном пространстве с течением времени изменилось. Зафиксируем его новое местоположение (рис 5.):

А теперь, мы проводим вектора, которые соединяют местоположение точек в прошлом и в настоящем. Получаем тессеракт (рис. 6):

Рис. 6 Тессеракт (построение)

Подобным образом строятся остальные гиперкубы, конечно же учитывается смысл пространства, в котором гиперкуб находится.

Как насчет 10D?

В 1919 году польский математик Теодор Калуца предположил, что существование четвертого пространственного измерения может увязать между собой общую теорию относительности и электромагнитную теорию. Идея, впоследствии усовершенствованная шведским математиком Оскаром Кляйном , заключалась в том, что пространство состояло как из «расширенных» измерений, так и из «свернутых» измерений. Расширенные измерения — это три пространственных измерения, с которыми мы знакомы, и свернутое измерение находится глубоко в расширенных размерах. Эксперименты позже показали, что свернутое измерение Калуцы и Кляйна не объединило общую теорию относительности и электромагнитную теорию, как это первоначально предполагалось, но спустя десятилетия теоретики теории струн нашли эту идею полезной, даже необходимой.

Математика, используемая в теории суперструн, требует не менее 10 измерений. То есть для уравнений, описывающих теорию суперструн и для того чтобы связать общую теорию относительности с квантовой механикой, для объяснения природы частиц, для объединения сил и т. д. — необходимо использовать дополнительные измерения. Эти измерения, по мнению теоретиков струн, завернуты в свернутое пространство, изначально описанное Калуцей и Кляйном.

Круги представляют собой дополнительный пространственный размер, свернутый в каждую точку нашего знакомого трехмерного пространства. │ WGBH / NOVA

Чтобы расширить скрученное пространство, чтобы включить эти добавленные размеры, представьте, что круги Калуцы-Клейна заменяются сферами. Вместо одного добавленного измерения мы имеем два, если рассматривать только поверхности сфер и три, если учесть пространство внутри сферы. Получилось всего шесть измерений. Так где же другие, которые требует теория суперструн?

Оказывается, что до того, как появилась теория суперструн, два математика Эудженио Калаби из Университета Пенсильвании и Шин-Тунг Яу из Гарвардского университета описали шестимерные геометрические формы. Если мы заменим сферы в скрученном пространстве этими формами Калаби-Яу, мы получим 10 измерений: три пространственных, а также шестимерные фигуры Калаби-Яу .

Шестимерные формы Калаби-Яу могут объяснять дополнительные размеры, требуемые теорией суперструн. │ WGBH / NOVА

Приверженцы теории струн делают ставку на то, что дополнительные измерения действительно существуют. На самом деле, уравнения, описывающие теорию суперструн, предполагают вселенную с не менее чем 10 измерениями. Но даже физикам, которые все время думают о дополнительных пространственных измерениях сложно описать как они могут выглядеть, или как люди могли бы приблизиться к их пониманию.

Если теория суперструн будет доказана и идея мира, состоящего из 10 или более измерений, подтвердится, то появится ли когда-нибудь объяснение или визуальное представление более высоких измерений, которые сможет постичь человеческий разум? Ответ на этот вопрос навсегда может стать отрицательным, если только какая-то четырехмерная жизненная форма не «вытащит» нас из нашего трехмерного мира и не даст нам увидеть мир с ее точки зрения.

В котором просим наших ученых ответить на довольно простые, на первый взгляд, но спорные вопросы читателей. Для вас мы выбрали самые интересные ответы экспертов ПостНауки.

Всем знакомо сокращение 3D, означающее «трёхмерный» (буква D — от слова dimension — измерение). Например, выбирая в кинотеатре фильм с пометкой 3D, мы точно знаем: для просмотра придётся надеть специальные очки, но зато картинка будет не плоской, а объёмной. А что такое 4D? Существует ли «четырёхмерное пространство» в реальности? И можно ли выйти в «четвёртое измерение»?

Чтобы ответить на эти вопросы, начнём с самого простого геометрического объекта — точки. Точка нульмерна. У неё нет ни длины, ни ширины, ни высоты.

// 8-cell-simple

Сдвинем теперь точку по прямой на некоторое расстояние. Допустим, что наша точка — остриё карандаша; когда мы её сдвинули, она прочертила отрезок. У отрезка есть длина, и больше никаких измерений: он одномерен. Отрезок «живёт» на прямой; прямая является одномерным пространством.

Возьмём теперь отрезок и попробуем его сдвинуть так, как раньше точку. Можно представить себе, что наш отрезок — это основание широкой и очень тонкой кисти. Если мы выйдем за пределы прямой и будем двигаться в перпендикулярном направлении, получится прямоугольник. У прямоугольника есть два измерения — ширина и высота. Прямоугольник лежит в некоторой плоскости. Плоскость — это двумерное пространство (2D), на ней можно ввести двумерную систему координат — каждой точке будет соответствовать пара чисел. (Например, декартова система координат на школьной доске или широта и долгота на географической карте.)

Если сдвинуть прямоугольник в направлении, перпендикулярном плоскости, в которой он лежит, получится «кирпичик» (прямоугольный параллелепипед) — трёхмерный объект, у которого есть длина, ширина и высота; он расположен в трёхмерном пространстве, в таком, в каком живём мы с вами. Поэтому мы хорошо представляем себе, как выглядят трёхмерные объекты. Но если бы мы жили в двумерном пространстве — на плоскости, — нам пришлось бы изрядно напрячь воображение, чтобы представить себе, как можно сдвинуть прямоугольник, чтобы он вышел из той плоскости, в которой мы живём.

Представить себе четырёхмерное пространство для нас также довольно непросто, хотя очень легко описать математически. Трёхмерное пространство — это пространство, в котором положение точки задаётся тремя числами (например, положение самолёта задаётся долготой, широтой и высотой над уровнем моря). В четырёхмерном же пространстве точке соответствует четвёрка чисел-координат. «Четырёхмерный кирпич» получается сдвигом обычного кирпичика вдоль какого-то направления, не лежащего в нашем трёхмерном пространстве; он имеет четыре измерения.

На самом деле мы сталкиваемся с четырёхмерным пространством ежедневно: например, назначая свидание, мы указываем не только место встречи (его можно задать тройкой чисел), но и время (его можно задавать одним числом, например количеством секунд, прошедших с определенной даты). Если посмотреть на настоящий кирпич, у него есть не только длина, ширина и высота, но ещё и протяженность во времени — от момента создания до момента разрушения.

Физик скажет, что мы живём не просто в пространстве, а в пространстве-времени; математик добавит, что оно четырёхмерно. Так что четвёртое измерение ближе, чем кажется.

Тема многомерности пространства, в котором мы живем, давно уже привлекала внимание художников и искусствоведов. Многомерность, выход за привычные представления, открывает, казалось бы, новые и многообещающие возможности. Некоторые искусствоведы утверждали даже в начале века, что без учета многомерности пространства понять современное искусство нельзя. По этому поводу уместно сделать два замечания.

Во-первых, многомерность понимается всегда как четырехмерность, то есть существование наряду с обычными тремя пространственными измерениями (нагляднее всего их можно представить себе как смещения в трех направлениях; вверх-вниз, вперед-назад и влево-вправо) и еще одного, четвертого. За это новое измерение принимали время. Это имело известные основания, поскольку в начале века появилась теория относительности с ее понятием единого пространственно- временного континуума. Однако надо понимать, что если исходить из современной физики, то для нашей обычной жизни, обычных скоростей и расстояний, теория относительности приобретает банальный облик привычного из школьных представлений пространства и независимо от него текущего времени. И это даже в том случае, если за обычные скорости и расстояния взять размеры Солнечной системы и скорости движения планет. Поэтому теория относительности в передаче обычной человеческой жизни, основной темы художников, ничего изменить не должна.

Вторым моментом, который хотелось бы отметить, является то, что значительно более сложное четырехмерное пространство, где четвертой координатой является не время (что себе легко представить), а тоже пространственная координата (что представить себе немыслимо), уже давно привлекло внимание художников. Более того, они даже разработали успешные методы его изображения. Речь идет об иконописцах в основном XV столетия » в это время передача четырехмерного пространства достигла наибольшего совершенства в русской иконописи.

Прежде чем переходить к рассмотрению соответствующих икон, необходимо дать ряд пояснений геометрического характера, чтобы общие рассуждения о четырехмерном пространстве и возможных способах его изображения приобрели наглядность. Главная трудность в наглядном описании геометрии четырехмерного пространства связана с тем, что представить себе его нельзя. Это невозможно, поскольку требует от нас кроме естественных трех направлений (о них уже говорилось: направления вперед-назад, влево-вправо и вверх-вниз) представить себе движение в «четвертом» направлении, но такое, при котором в трех естественных направлениях движения не происходит. Иными словами, для нас, существ трехмерных, точка будет видна неподвижной, а на самом деле она будет двигаться в «четвертом» направлении. Единственный метод, который может здесь помочь,» это метод аналогий. Будем исходить из того, что наш привычный трехмерный мир «вложен» в четырехмерное пространство, что легко описать словами, но представить себе нельзя. Но зато ничего не стоит представить себе аналогичную, но элементарно простую ситуацию: двухмерный мир, «вложенный» в трехмерный. Хотя бы лист бумаги, находящийся в привычном для нас трехмерном пространстве.

Пусть теперь этот лист бумаги будет тем двухмерным «пространством», на котором живут некие «плоские» существа, могущие ползать по листу; плоские существа, ползающие по плоскому листу, » аналогия нас, трехмерных организмов, перемещающихся в трехмерном пространстве. Пусть этот лист будет безграничным, а по его обеим сторонам ползают эти самые плоские существа: одни с верхней стороны листа, другие » с нижней. Совершенно очевидно, что, сколько бы они ни ползали, верхние никогда не встретятся с нижними, хотя они могут быть бесконечно близки друг к другу » ведь их все равно будет разделять бесконечно тонкая толщина непроницаемого листа. Таким образом, каждую точку листа надо будет считать дважды » как принадлежащую верхней и как принадлежащую нижней стороне. Естественно, что на верхней стороне листа могут происходить одни, а на нижней » другие события, причем эти события не будут мешать друг другу, поскольку они сдвинуты относительно друг друга хотя и на бесконечно малую величину, но в «непостижимом» для плоских существ направлении » перпендикулярно поверхности листа. Эта «непостижимость» обусловлена для плоских существ тем, что последние никогда в своей жизни в таком направлении не перемещались и перемещаться не могут.

Эти две стороны одного листа позволяют по аналогии представить себе одновременное существование в некотором месте, хотя бы в комнате, обычного и мистического пространства. В первом живут и действуют люди, а во втором, например, ангелы. И те, и другие существуют в своих трехмерных пространствах и действуют, не мешая друг другу, поскольку эти два пространства «сдвинуты» относительно друг друга хотя и на бесконечно малую величину, но в непостижимом для людей «четвертом» направлении (напомним сделанное выше предположение, что наше обычное пространство «вложено» в четырехмерное). И в этом случае каждую точку подобной условной комнаты надо будет считать дважды » как принадлежащую мистическому и одновременно обычному пространству. Здесь полная аналогия с плоским листом, вложенным» в трехмерное пространство. Ведь можно для полноты аналогии условиться, что верхняя сторона листа является мистической, а нижняя » обычной поверхностью.

Графическое изображение четырёхмерного пространства

Современная наука представляет окружающий нас мир в форме трёхмерного пространства-времени (четырёхмерного пространства). Дать определение понятию «время» достаточно сложно, несмотря на очевидность его существования. Термин «стрела времени» характеризует его как ось, направленную из прошлого в будущее. Строго говоря, считать время четвертым измерением пространства нельзя, т.к. по правилам математики оно должно быть одновременно перпендикулярно всем трем имеющимся координатным осям.

Созданием трёхмерного пространства-времени (четырехмерного пространства) мы обязаны Генриху Минковскому. В 1908 году немецкий математик, развивая идеи теории относительности А.Эйнштейна заявил: «Отныне пространство само по себе и время само по себе должны обратиться в фикции, и лишь некоторый вид соединения обоих должен ещё сохранить самостоятельность».

По другой версии — «Минковский и Эйнштейн посчитали, что трёхмерное пространство и время в отдельности не существуют и что реальный мир является четырёхмерным ».

Таким образом, два гражданина для обоснования (развития) своих личных гипотез сложили в нарушение законов математики в единое целое три взаимно перпендикулярных координатных оси и условную сравнительную меру — время . (Более подробно о времени — Википедия http://ru.wikipedia.org/wiki/Время). Данное сложение можно сравнить со складыванием кирпичей с ананасами или литров с амперами. Очевидно, что подобное сложение противоречит здравому смыслу. Впрочем, сами физики не отрицают, что основным критерием современной физики является не здравый смысл, а «красота» физической теории.

ВЫВОД : Фундаментом всей современной физики является частное мнение одного гражданина или договоренность двух граждан. Заявленная ими гипотеза трёхмерного пространства-времени, как четырёхмерного пространства, противоречит элементарным основам математики и не имеет какого-либо обоснования.

Понятно, что теоретическая физика на тот момент времени оказалась в тупике и дальнейшие пути развития были весьма туманны. Нужно было что-то делать и поэтому за предложенную гипотезу ухватились, как за промежуточный вариант выхода из кризиса. Известная поговорка гласит, что нет ничего более постоянного, чем временные решения. К сожалению, ничего альтернативного предложено не было, и физика пошла по предложенному пути, как по единственно возможному. Признание научным сообществом данной гипотезы вызвало бурное развитие физики — многомерные пространства, кротовые норы, путешествия во времени и т.д. Автор этих строк считает верхом мудрости современной физики следующий научный перл — «семимерная сфера в одиннадцатимерном пространстве»… Возникает вопрос: чего стоят «достижения» современной науки с таким сомнительным фундаментом — теория относительности, квантовая механика (которую не понимают даже её авторы), чёрные дыры, теории Большого Взрыва и расширения Вселенной, супергравитация, теория струн, тёмная материя и тёмная энергия..? Нарастающая в прессе критика существующего положения свидетельствует о том, что возникший более ста лет тому назад кризис в физике так и не был преодолен. Причина одна — безальтернативная гипотеза трёхмерного пространства-времени (четырёхмерного пространства) по-прежнему остается фундаментом здания современной физики.

Для понимания физической сущности четырёхмерного пространства и возможности его графического изображения нам придется вернуться к основам научных знаний.

1. Нулевое пространство

(пространство с количеством измерений, равным нулю).

Нулевое пространство является математической точкой.

Материал из Википедии : «В геометрии, топологии и близких разделах математики точкой называют абстрактный объект в пространстве, не имеющий ни объёма, ни площади, ни длины, ни каких-либо других измеримых характеристик. Таким образом, точкой называют нульмерный объект . Точка является одним из фундаментальных понятий в математике; любая геометрическая фигура считается состоящей из точек . Евклид определил точку как то, что не имеет измерений. В современной аксиоматике геометрии точка является первичным понятием, задаваемым перечнем его свойств».

Проведем эксперимент: любым удобным способом сложим (соединим, совместим и т.п., например, проведем несколько линий через одну точку) несколько математических точек до их полного совпадения. Формула подобного сложения выглядит следующим образом:

В результате наших действий первоначальная математическая точка, как и остальные математические точки, используемые в этом сложении, не изменилась в размерах и соответственно не приобрела измерений. При участии в этом эксперименте бесконечного количества математических точек результат также не изменится.

Формула нулевого пространства (математической точки)

Обозначим нулевое пространство (математическую точку) — 0ПР , тогда:

ВЫВОДЫ:

Любая математическая точка является свернутой бесконечностью состоящей из сложенных (совмещенных) математических точек. В свою очередь, каждая из математических точек входящих в эту бесконечность является отдельной самостоятельной бесконечностью и т.д.

Математическая точка — это бесконечное множество свернутых бесконечностей — «бесконечность бесконечностей».

НУЛЕВОЕ ПРОСТРАНСТВО СОСТОИТ ИЗ «БЕСКОНЕЧНОСТИ БЕСКОНЕЧНОСТЕЙ» СЛОЖЕННЫХ НУЛЕВЫХ ПРОСТРАНСТВ.

2. Одномерное пространство.

Одномерное пространство является линией.

Линия, согласно учебнику геометрии, состоит из бесконечного количества математических точек. В рамках настоящей работы это означает, что линия состоит из бесконечного количества нулевых пространств . Очевидно, что формула сложения (совмещения) математических точек — 0 + 0 + 0 + … + 0 = 0 — действительная для нулевого пространства, не может быть использована для образования одномерного пространства в виде линии. Все математические точки образующие линию должны быть в результате какого-то действия разъединены (отделены) друг от друга. Обозначим это неизвестное действие, разъединяющее соседние математические точки в линии, буквой «и». Очевидно, что действие, разъединяющее математические точки в линии, не может являться любым из известных действий в математике типа «сложить», «умножить», «разделить» и т. п.

Формула одномерного пространства (1ПР) будет выглядеть следующим образом:

Положение любой произвольной точки на линии, относительно точки выбранной в качестве начала координат, определяется одним измерением — «x ».

Линия состоит из бесконечного количества разъединённых математических точек.

ОДНОМЕРНОЕ ПРОСТРАНСТВО СОСТОИТ ИЗ БЕСКОНЕЧНОГО КОЛИЧЕСТВА РАЗЪЕДИНЁННЫХ НУЛЕВЫХ ПРОСТРАНСТВ.

3. Двухмерное пространство.

Двухмерное пространство является плоскостью.

Двухмерное пространство представляет собой плоскость, состоящую из бесконечного количества линий или из бесконечного количества одномерных пространств. Очевидно, что для образования плоскости соседние линии (одномерные пространства) также должны быть разъединены во избежание их сложения (совмещения).

Формула двухмерного пространства (2ПР) будет выглядеть следующим образом:

1ПР и 1ПР и 1ПР и. .. и 1ПР = 2ПР (плоскость)

Положение любой произвольной точки на плоскости относительно точки выбранной в качестве начала координат определяется двумя измерениями — «x » и «y ».

ДВУХМЕРНОЕ ПРОСТРАНСТВО СОСТОИТ ИЗ БЕСКОНЕЧНОГО КОЛИЧЕСТВА РАЗЪЕДИНЁННЫХ ОДНОМЕРНЫХ ПРОСТРАНСТВ.

4. Трёхмерное пространство.

Трёхмерное пространство является заполненным объёмом.

Трёхмерное пространство представляет собой объём, состоящий из бесконечного количества плоскостей или из бесконечного количества двухмерных пространств. Также очевидно, что для образования заполненного объема соседние плоскости (двухмерные пространства) должны быть разъединены во избежание их сложения (совмещения).

Формула трёхмерного пространства (3ПР) будет выглядеть следующим образом:

Положение любой произвольной точки в заполненном объёме, относительно точки, выбранной в качестве начала координат, определяется тремя измерениями — «x », «y » и «z ».

ТРЁХМЕРНОЕ ПРОСТРАНСТВО СОСТОИТ ИЗ БЕСКОНЕЧНОГО КОЛИЧЕСТВА РАЗЪЕДИНЁННЫХ ДВУХМЕРНЫХ ПРОСТРАНСТВ.

Из изложенного видно, что пространства с большей мерностью состоят из бесконечного множества разъединённых пространств меньшей мерности — одномерное из разъединённых нулевых, двухмерное из разъединённых одномерных, трёхмерное из разъединённых двухмерных.

В свою очередь, четырёхмерное пространство должно состоять из бесконечного множества разъединённых трёхмерных пространств. Однако это невозможно по очевидной причине — если имеется одно бесконечное трёхмерное пространство, каждое из измерений которого равно бесконечности (x = y = z = ∞) , то отсутствует место для размещения любого другого трёхмерного пространства, разъединённого с данным. В имеющемся трёхмерном пространстве можно выделить любой больший или меньший заполненный объём, но он будет являться только частью данного трёхмерного пространства.

ВЫВОД:

Создание четырёхмерного пространства из бесконечного множества разъединённых трёхмерных пространств невозможно.

Для того чтобы понять, какое пространство нас окружает, необходимо разобраться в сложении и разъединении пространств, предварительно разобравшись в различии между объёмом (геометрическим объёмом, трёхмерным объёмом) и трёхмерным пространством.

Сложилось устойчивое мнение, что объёмные фигуры в форме параллелепипеда, шара, конуса, пирамиды и т.п. представляют собой трёхмерное пространство:

При внимательном рассмотрении видно, что параллелепипед представляет собой набор из шести плоскостей (шести двухмерных пространств), а шар представляет собой одну изогнутую плоскость (одно изогнутое двухмерное пространство) и обе эти фигуры не являются трёхмерными пространствами. Толщина плоскости (стенки) в любой из этих фигур равна одной математической точке. Внутри каждой из фигур находится пустота.

В качестве аналогии можно привести пример с аквариумом в форме параллелепипеда. Если аквариум пуст, то в него можно вставить другой аквариум несколько меньших размеров:

Отличие трёхмерного объема от трёхмерного пространства можно понять на следующем примере. Если в больший по размерам аквариум налить воды, то вставить в него меньший по размеру аквариум будет невозможно — т.к. его пространство занято водой. Аквариум заполненный водой является трёхмерным пространством, а пустой аквариум является трёхмерным объёмом.

Трёхмерное пространство можно представить себе в форме параллелепипеда (x = y = z = ∞) , весь объём которого заполнен двухмерными пространствами (параллельными плоскостями), каждое из которых имеет толщину в одну математическую точку:

ВЫВОДЫ:

Объём (трёхмерный объём, геометрический объём) представляет собой абстрактное понятие в форме пустоты, ограниченной двухмерными пространствами.

Трёхмерное пространство состоит из бесконечного множества разъединённых двухмерных пространств, каждое из которых состоит из бесконечного множества разъединённых одномерных пространств, каждое из которых в свою очередь состоит из бесконечного множества разъединённых нулевых пространств.

ТРЕХМЕРНОЕ ПРОСТРАНСТВО ПРЕДСТАВЛЯЕТ СОБОЙ РЕАЛЬНЫЙ ФИЗИЧЕСКИЙ ОБЪЕКТ В ВИДЕ ТРЁХМЕРНОГО ГЕОМЕТРИЧЕСКОГО ОБЪЁМА, КАЖДОЕ ИЗ ИЗМЕРЕНИЙ КОТОРОГО РАВНО БЕСКОНЕЧНОСТИ, ЗАПОЛНЕННЫЙ ПО КАЖДОМУ ИЗМЕРЕНИЮ БЕСКОНЕЧНЫМ МНОЖЕСТВОМ РАЗЪЕДИНЁННЫХ НУЛЕВЫХ ПРОСТРАНСТВ.

ТРЁХМЕРНОЕ ПРОСТРАНСТВО НЕ МОЖЕТ СОДЕРЖАТЬ В СЕБЕ ПУСТОТУ В ВИДЕ ПУСТОГО КОСМОСА, ПУСТОГО ВАКУУМА И Т.Д.

Возникает противоречие — или верны основы научных знаний и окружающее нас пространство из чего-то состоит (материя, эфир, элементы физического вакуума, тёмная материя или что-то иное), или верна теория А.Эйнштейна с его абсолютной пустотой трёхмерного пространства-времени.

Сложение пространств можно представить в следующем виде. Возьмём нулевое пространство (математическую точку) в форме ящика (параллелепипеда) без крышки, все измерения которого равны нулю, и толщина стенок также равна нулю:

Очевидно, что внутрь этого ящика можно вставить бесконечное количество подобных ящиков, ведь его и их размеры и толщина стенок равны нулю:

Данное действие можно сравнить с вкладыванием друг в друга одноразовых стаканчиков или матрёшек, но при этом количество вкладываемых стаканчиков или матрёшек равно бесконечности. Подобное вкладывание можно представить себе в следующей форме (все размеры ящиков равны нулю):

Вывод: Cложение нулевых пространств — это действие по совмещению (наложению) бесконечного множества нулевых пространств без изменения их первоначальных размеров.

Сложение нулевого пространства со множеством нулевых пространств не требует какой-либо упорядоченности или последовательности действий.

Очевидно, что абстрактные нулевые, одно, двух и трёхмерные пространства могут складываться между собой в любом сочетании — т.к. все они в основе состоят из математических точек (нулевых пространств). Абстрактными эти пространства называются потому, что взаимное расположение точек, из которых они состоят, принимается в качестве исходного условия. Нулевое пространство можно сложить с трёхмерным или одномерное сложить с двухмерным или трёхмерное сложить с трёхмерным (последовательно, точку с точкой каждого из пространств). Сложение пространств означает сворачивание пространства с большей мерностью в пространство с меньшей мерностью . При сложении двух или более пространств с одинаковой мерностью остается только одно пространство с первоначальной мерностью. Сложение абстрактных пространств не требует приложения усилий или энергетических затрат. Идеальным состоянием (идеальным пространством) является сложение всех абстрактных нулевых, одно, двух и трёхмерных пространств в одно нулевое пространство (в одну математическую точку).

Создание (образование) реальных одно, двух и трёхмерных пространств требует обязательного возникновения какого-то действия, позволяющего удерживать соседние математические точки (нулевые пространства) от сложения. Такое действие обозначено в настоящей работе знаком «и » и называется в отличие от других математических операций «Разъединение ».

Существование «разъединения» математических точек подтверждается самим фактом существования окружающего нас мира. Если бы данного действия не было, то окружающий нас мир мгновенно свернулся бы в одну математическую точку (в одно нулевое пространство) и прекратил бы своё существование. Разъединение математических точек и пространств является принципиально новым действием, при котором возникает препятствие к сложению пространств (сложению математических точек).

Любая математическая точка (нулевое пространство) состоит, как было показано ранее, из бесконечного количества сложенных математических точек (нулевых пространств). Рассмотрим, в качестве примера, нулевое пространство, состоящее из двух нулевых пространств:

Единственным способом (по мнению автора) разъединить соседние математические точки — нулевые пространства (т.е. создать пространство более высокого уровня) является придание им противоположных направлений вращения:

Более наглядно это можно представить на примере встречного вращения нулевых пространств в форме шара с диаметром, равным нулю:

Рассмотрим сущность вращения более подробно:

а) Вращение математической точки вокруг одной оси координат будет представлять собой плоскую фигуру — окружность .

б) вокруг двух осей координат будет представлять собой объемную фигуру — шар (сферу) .

в) Вращение математической точки одновременно вокруг трёх осей координат будет представлять собой — вращающийся шар .

Одновременное вращение точки вокруг трёх осей координат равнозначно вращению этой точки вокруг одной дополнительной оси «F», проходящей через начало координат.

Более наглядно вращение точки вокруг одной дополнительной оси «F », проходящей через начало координат, как её одновременное вращение вокруг трёх осей координат, можно представить в следующем виде:

Плоскости вращения V x , V y и V z перпендикулярны поверхности вращающегося шара, образованного V x,y,z .

Дополнительная ось «F» вращения V x,y,z проходит через начало координат «0», но в общем случае не совпадает ни с одной из координатных осей. Положение оси «F» относительно осей координат определяется значением V x , V y и V z .

Вывод:

Любое вращение перпендикулярно одновременно всем трём осям координат.

Вращение в зависимости от направления (по или против часовой стрелки) может изменяться от 0 до –N и от 0 до +N , где N — число оборотов вращения или скорость вращения (направление вращения по часовой стрелке обозначим знаком «плюс», а против часовой знаком «минус»).

Вывод:

Вращение является четвёртым измерением пространства.

Кинетическая энергия вращения материального тела (например маховика) определяется по формуле:

Следовательно, вращение представляет собой энергию . Отсюда можно сделать вывод:

ЧЕТЫРЕХМЕРНОЕ ПРОСТРАНСТВО ЯВЛЯЕТСЯ «ПРОСТРАНСТВОМ-ЭНЕРГИЕЙ».

Графически четырёхмерное «пространство-энергию» можно представить в следующем виде:

Очевидно, что существование данного четырёхмерного пространства нарушает энергетический баланс. Соответственно, реальное физическое четырёхмерное пространство должно состоять только из чётного количества энергий с противоположными направлениями вращения, сумма которых равна нулю :

Рассмотрим сущность вращения. Для вращения металлического шара необходимо наличие оси вращения — отверстие в шаре, ось, подшипники, опоры или необходимы вал, подшипники, опоры и прочее, в зависимости от технического решения. Для четырёхмерного пространства проблему обеспечения самой возможности вращения противоположных энергий вокруг оси можно решить только в случае представления этих энергий в форме противоположно направленных вращающихся вихревых торов:

Графически реальное физическое четырёхмерное «пространство — энергия» можно представить в виде объёма, образованного двумя энергиями с противоположными направлениями вращения:

Четырехмерное пространство представляет собой объем (V = π · D2 · L / 4), заполненный энергией (встречное осевое и круговое вращение правого и левого вихревых торов).

Возникновение четырёхмерного «пространства-энергии» (разъединение двух соседних математических точек внутри одной математической точки ) можно представить следующим образом:

ОКРУЖАЮЩИЙ НАС МИР — ЭТО БЕСКОНЕЧНЫЙ ТРЁХМЕРНЫЙ ОБЪЕМ, ЗАПОЛНЕННЫЙ БЕСКОНЕЧНЫМ КОЛИЧЕСТВОМ ЕДИНИЧНЫХ ЧЕТЫРЁХМЕРНЫХ ПРОСТРАНСТВ, ОБРАЗОВАННЫХ ПРАВЫМИ И ЛЕВЫМИ ВИХРЕВЫМИ ТОРАМИ, СОСТОЯЩИМИ ИЗ ЭНЕРГИИ ВРАЩЕНИЯ.

Окружающий нас мир представляет собой четырёхмерное «пространство-энергию», состоящее из бесконечного множества разъединённых единичных четырёхмерных пространств:

Окружающий нас мир является четырёхмерным «пространством-энергией» и имеет четыре измерения.

Любая точка четырёхмерного «пространства-энергии» характеризуется местом её нахождения и величиной энергии относительно точки выбранной в качестве начала координат:

Место нахождения любой точки определяется тремя измерениями в виде линейных координат «X», «Y», «Z» .

Величина энергии «Е» в любой точке определяется одним измерением — сравнением с величиной энергии в точке, взятой в качестве начала координат.

Четырёхмерное «пространство-энергия» не имеет начала или конца, все точки этого пространства абсолютно равноправны и, соответственно, в этом пространстве не может быть выделенной (привилегированной) системы координат.

Окружающий нас мир будет выглядеть следующим образом:

ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ОБРАЗОВАНИЯ ОКРУЖАЮЩЕГО НАС ЧЕТЫРЁХМЕРНОГО МИРА, СОСТОЯЩЕГО ИЗ МНОЖЕСТВА ЧЕТЫРЁХМЕРНЫХ ПРОСТРАНСТВ ВНУТРИ ОДНОЙ МАТЕМАТИЧЕСКОЙ ТОЧКИ (НУЛЕВОГО ПРОСТРАНСТВА) , как аналог БОЛЬШОГО ВЗРЫВА выглядит следующим образом:

С учетом того, что развёрнутая бесконечность внутри математической точки представляет собой два бесконечных множества правых и левых вихревых торов в форме энергии, можно утверждать, что свёрнутая бесконечность развернулась в две противоположные бесконечности — правую и левую .

Разъединение всего лишь двух математических точек сразу приводит к образованию единичного четырёхмерного пространства. Объём состоит из площади умноженной на длину. Заполненный объём состоит из энергии, являющейся четвертым измерением. Площадь и длина образуются при встречном движении энергий. Следовательно, невозможно наличие в нашем мире одно, двух и трёхмерных пространств , что прекрасно подтверждается на практике. Также, невозможно возникновение в нашем мире пространств с мерностью более четырёх по ранее указанной причине — отсутствие места для их нахождения.

Очевидно, что вихревые торы образующие четырёхмерное пространство, и имеющие одинаковые составляющие направления вращения, могут образовывать более сложные конструкции — правые и левые вихревые трубки. Вихревые трубки могут замыкаться в правые и левые вихревые кольца, что приводит к образованию различных вихревых цепочек из правых и левых вихревых колец:

Наличие вихревых цепочек позволяет (путем самосборки) создать из них относительно устойчивых вихревые структуры в форме шара (сферы), тора и т.п. Дальнейшее усложнение структуры пространства на одном из этапов приводит к формированию структур, которые мы называем электронами, протонами и далее к формированию вещества, планет, звезд, галактик и т.д.

Некоторые определения:

РАЗЪЕДИНЕНИЕ — ЭТО РАЗДЕЛЕНИЕ НА ЛЕВОЕ И ПРАВОЕ.

ВРАЩЕНИЕ ≡ ЭНЕРГИЯ

ЭНЕРГИЯ ДЕЛИТСЯ НА ДВА ВИДА:
— правая энергия (энергия вращения правого вихревого тора)
— левая энергия (энергия вращения левого вихревого тора)

ПРОСТРАНСТВО — ЭТО БЕСКОНЕЧНЫЙ ТРЁХМЕРНЫЙ ОБЪЁМ, ОБРАЗОВАННЫЙ ЭНЕРГИЯМИ БЕСКОНЕЧНОГО КОЛИЧЕСТВА ПРАВЫХ И ЛЕВЫХ ВИХРЕВЫХ ТОРОВ.

МАТЕРИЯ — ЭТО ЭЛЕМЕНТАРНАЯ ЕДИНИЦА ПРОСТРАНСТВА, ОБРАЗОВАННАЯ ПРИ РАЗЪЕДИНЕНИИ ДВУХ СОСЕДНИХ МАТЕМАТИЧЕСКИХ ТОЧЕК (ДВУХ НУЛЕВЫХ ПРОСТРАНСТВ) И СОСТОЯЩАЯ ИЗ ПРАВОЙ И ЛЕВОЙ ЭНЕРГИЙ.

ПРОСТРАНСТВО ОБРАЗОВАНО МАТЕРИЕЙ.

РАЗМЕРЫ МАТЕРИИ СТРЕМЯТСЯ К НУЛЮ.

— ДВА ВИДА ЭНЕРГИИ ОБРАЗУЮТ ПРОСТРАНСТВО.

— ПРОСТРАНСТВО ОБРАЗОВАНО ДВУМЯ ВИДАМИ ЭНЕРГИИ.

ОКРУЖАЮЩИЙ НАС МИР ДВОИЧЕН В СВОЕЙ ОСНОВЕ.

В ОКРУЖАЮЩЕМ НАС МИРЕ НЕТ НИЧЕГО КРОМЕ ЭНЕРГИИ.

В настоящей работе введение четвертого измерения пространства в виде энергии «Е» обязывает пересмотреть мерность традиционных пространств в форме линии, плоскости и заполненного объема:

— Линия, является абстрактным двухмерным пространством . Координаты любой точки на линии, относительно точки выбранной в качестве начала координат, определяются двумя измерениями: «x » — длины и «е » — энергии.

— Плоскость, является абстрактным трёхмерным пространством . Координаты любой точки на плоскости, относительно точки выбранной в качестве начала координат, определяются тремя измерениями — «x » — длины, «y » — ширины и «е » — энергии.

— Заполненный объём, является реальным четырёхмерным пространством . Координаты любой точки заполненного объема, относительно точки выбранной в качестве начала координат, определяются четырьмя измерениями — «x » — длины, «y » — ширины, «z » — высоты и «е » — энергии.

Одномерного пространства не существует, т.к. любое сравнение выбранной точки с точкой начала координат требует выполнения сразу двух измерений — энергии и взаимного расположения.

Выше по тексту утверждалось, что создать четырёхмерное пространство невозможно. Кажется, что возникает противоречие, однако это не так. В абстрактных пространствах — одномерное (линия), двухмерное (плоскость) и трёхмерное (объём) — взаимное положение точек задается в качестве исходного условия. В любом реальном физическом пространстве соседние точки пространства должны быть отделены (разъединены) друг от друга. В противном случае все точки (пространства) сольются в одну математическую точку. В качестве механизма их разъединения предложено «РАЗЪЕДИНЕНИЕ» в форме наделения соседних математических точек противоположными (правыми и левыми) энергиями. Как было показано, энергия является четвёртым измерением пространства. Таким образом, никакого противоречия нет — к существующим традиционным измерениям пространств просто добавлен в виде дополнительного измерения механизм разъединения соседних математических точек. Абстрактные одно, двух и трёхмерные пространства переводятся в реальные пространства путем добавления к любому из них механизма разъединения соседних математических точек в форме четвёртого измерения. В процессе перевода выяснилось, что разъединение в любом из этих пространств двух соседних математических точек приводит к одному результату — возникновению четырёхмерного пространства-энергии.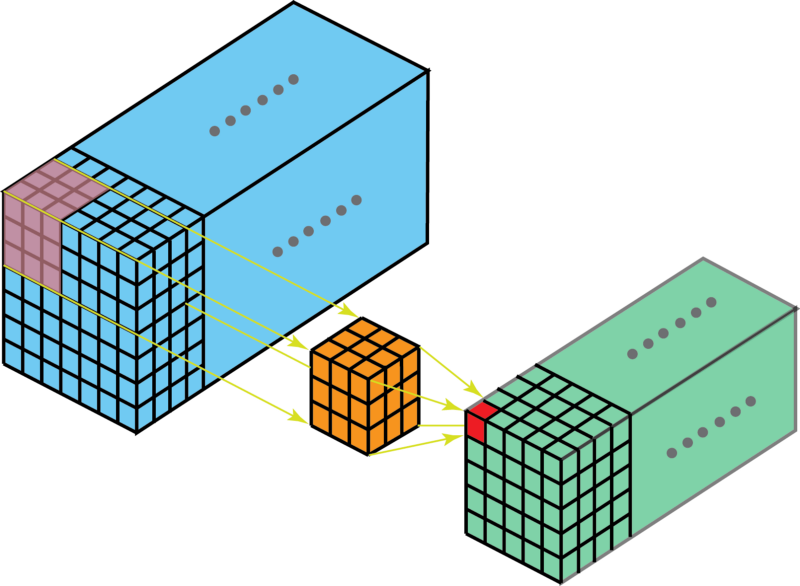 Соответственно, реальным физическим пространством может быть только четырёхмерное пространство-энергия. Все остальные пространства могут быть только абстрактными, что прекрасно подтверждается на практике в виде окружающего нас четырёхмерного мира.

Ранее было показано, что без «Разъединения» все пространства и все математические точки сложатся в одну общую точку. Назовем эту точку — «Математической точкой НАЧАЛА». «Математическая точка НАЧАЛА» представляет собой объект, вокруг которого ничего нет — ни вещества, ни пространства, ни энергии, ни пустоты, ни измерений, ни чего-либо иного, т.е. абсолютное НИЧТО или НОЛЬ. Внутри «Математическая точка НАЧАЛА» представляет собой свёрнутую «бесконечность бесконечностей» математических точек (нулевых пространств), также равную НУЛЮ. Таким образом, сохраняется равновесное состояние: ноль равен нулю. «Математическая точка НАЧАЛА» — это в принципе единственно возможный объект. Можно сказать, что это — «ЕДИНСТВЕННОЕ НАЧАЛО ВСЕГО» или, что это — «НАЧАЛО НАЧАЛ».

Возникновение четырёхмерного пространства из «Математической точки НАЧАЛА» (Начального нулевого пространства) следует понимать как качественное изменение состояния — переход одной свёрнутой «бесконечности бесконечностей» в две развёрнутые противоположные бесконечности с мгновенным образованием бесконечного четырёхмерного пространства, а не как постепенное заполнение энергией какого-то ранее существовавшего пустого объема. Бесконечное количество математических точек уже находились внутри одной «Математической точки НАЧАЛА» по определению, как свёрнутая бесконечность. Развёртывание двух противоположных бесконечностей происходит как фазовый переход внутри «Математической точки НАЧАЛА» — мгновенное возникновение из бесконечного количества нулевых пространств бесконечного четырёхмерного пространства, состоящего из двух видов энергии. При этом равновесное состояние не нарушается — сумма двух противоположных (встречных) бесконечностей остается равной нулю.

Разворачивание двух встречных бесконечностей в виде двух противоположных энергий — правой и левой, следует понимать как их взаимосвязь и тесное переплетение. Любая достаточно малая часть четырёхмерного пространства, вакуум, межзвездное пространство, любая элементарная частица и далее протоны, электроны, атомы, молекулы, вещество, планеты, звёзды и галактики состоят одновременно из двух видов энергии — правой и левой.

Объективное наличие в окружающем нас мире энергии, времени и трёх измерений пространства отрицать достаточно сложно.

Время является характеристикой энергии, показывающей последовательность изменения её величины в данной точке четырёхмерного пространства по отношению к точке, выбранной в качестве начала координат.

Очевидный вывод: Большого взрыва, расширения или сжатия Вселенной никогда не было и не будет. Теория относительности, чёрные дыры, тёмная материя и тёмная энергия, многомерность пространства и прочие «достижения» современной науки являются красивой оболочкой пустоты, на которой они построены.

Разъединение бесконечного количества соседних математических точек внутри одной «Математической точки НАЧАЛА» создает внутри неё четырёхмерное пространство заполненное энергиями. Сумма правой и левой энергий, образующих четырёхмерное пространство нашего мира, равна нулю. Это можно показать следующим образом:

Или 0 = 0

Таким образом, окружающий нас мир можно рассматривать или как флуктуацию НУЛЯ, или как флуктуацию свёрнутой бесконечности, равной нулю, которая разворачивается в две противоположных бесконечности, в сумме равные нулю, что по сути является такой же флуктуацией нуля. Если окружающий нас мир существует, то это значит, что вероятность разворачивания свёрнутой бесконечности в виде «Математической точки Начала» в две противоположные бесконечности больше нуля.

Формально окружающий нас мир или ВСЕЛЕННАЯ одновременно и бесконечен и равен нулю — для наблюдателя внутри нашего мира он вечен, бесконечен и не имеет границ, а для стороннего наблюдателя (если бы он мог находиться за пределами нашего мира) он равен нулю.

Стоит отметить, что «Математическая точка НАЧАЛА» является идеальным пространством и может существовать только в единственном экземпляре. Таким образом, при разъединении соседних математических точек внутри «Математической точки НАЧАЛА» происходит разворачивание двух противоположных бесконечностей и образуется только одна ВСЕЛЕННАЯ, вечная и бесконечная.

Графически четырёхмерное «Пространство — энергия» можно изобразить в следующем виде (точка «m» , выбранная в качестве начала координат, обладает энергией больше нуля):

Ни одна точка четырёхмерного пространства-энергии не может обладать энергией, равной нулю или меньшей нуля. Это объясняет причину того, что минимально возможная температура по шкале Цельсия равна –273 градуса, а величина максимальной температуры не имеет ограничения.

Несколько слов об эфире

Окружающий нас мир представляет собой структурированное четырёхмерное пространство-энергию — от кварков, протонов и электронов до звезд и звездных скоплений. Бесконечность наблюдаемого мира, как в сторону увеличения размеров объектов, так и в сторону их уменьшения, позволяет предположить общую структурированность четырёхмерного пространства, как его неотъемлемое свойство. В соответствии с этим, эфиром может быть названа энергетическая структура четырёхмерного пространства-энергии, расположенная ниже наблюдаемого (или ниже регистрируемого) на данный момент времени предельного размера объектов. Например, от кварков до элементарных единиц материи.

Авторские права на данную работу принадлежат
Фащевскому Александру Болеславовичу
[email protected] , http://afk-intech.ru/

фирменный стиль, который расширяет сознание и границы квадратных метров — Дизайн на vc.ru

1471 просмотров

SmartHeart завершил уже свой пятый по счету проект по брендингу с клиентом из Тюмени за последние 2 года. На этот раз агентство провело ребрендинг застройщика 4D. Команда агентства смогла создать визуальную систему, которая транслирует потребителям, что 4D — это больше возможностей и функциональных решений, а не просто квадратные метры.

Задача: обновить и не убить

Компания 4D Development существует на рынке с 2008 года. Застройщик известен своими проектами ЖК “Клевер Парк” и дизайн-квартал “МОЕ”. В портфеле 4D 105 000 кв.м. жилой и 2 530 кв.м. коммерческой недвижимости.

Задача, которая стояла перед агентством, состояла в том, чтобы создать сильный системный бренд, направленный на капитализацию и высокую конкурентность клиента не только на региональном, но и московском рынке. Визуальный стиль не должен был стать революционно другим, но должен был вывести застройщика на новый уровень бóльших возможностей.

Объем работ включал в себя разработку новой визуальной идентификации, платформы и архитектуры бренда,коммуникационную стратегию и оформление строй комплекса.

Платформа позиционирования: больше эмоций за те же деньги

Первое, что нужно было сделать при разработке платформы бренда — определить территорию позиционирования обновленного 4D. Для этого команда проекта проанализировала поле коммуникаций конкурентов и тщательно изучила самого клиента.

Глубинные интервью с командой заказчика выявили довольно прагматичное УТП — “потребителям нравятся наши планировки”. И само изначальное название компании 4D привело стратегов к формуле идеи: удачные планировки + 4D = увеличение пространства. Так родилась концепция “больше метров”, которая позже переросла в “больше места”, став эмоциональнее и живее.

Миссия бренда 4D — делать пространство функциональнее и продуманнее, чтобы независимо от квадратных метров жителям предоставлялось больше места для наполненной жизни.

Мы хотели прийти к балансу эмоционального и рационального восприятия, добавить бренду прагматики с заботой о себе: чтобы потребитель задумывался как о вложенных средствах, так и о своем комфорте и ощущении пространства. У нас получилось расширить, вывести процесс приобретения жилья за пределы покупки метров. С 4D люди могут позволить себе больше за те же деньги.

Роман Пустовойт

Дизайн: не революционный, а эволюционный

Творческая команда SmartHeart разработала 3 концепции разной степени смелости изменений фирменного стиля. Вместе с клиентом дизайнеры пришли к решению сохранить более сдержанную тональность айдентики. Заказчик хотел оставить визуальную идентичность бренда.

Преемственным элементом стала рамка, на основе которой SH сформировали всю дизайн-систему нового стиля. Целостная, она напоминает проектирование пространства для жизни. Рамка забрала в себя всю корпоративную идентификацию, навигационные комплексы, оформление строительных площадок, веб-пространства, онлайн коммуникаций. Этот минималистичный супер-простой прием размножился на такое количество имплементаций, что команде агентства пришлось создать сразу три брендбука вместо одного.

Был страх, что практичная структура дизайн-системы, может затянуть стиль в скуку, но как раз она позволила раскрыть его в многообразии сочетаний разного контента и фактур. Получилось органично, свежо и при этом без лишнего градуса экспериментальности.

Саша Орешонок

Логотип, наоборот, освободили от рамки в большинстве вариантов. Он не требовал сильного вмешательства: скорректировали пропорции, добавили воздуха, сделали его чуточку моднее. Шли по пути упрощения. Поскольку 4D уже известен в регионе, в дизайне можно было отбросить всё лишнее, тяжёлое и шумное без потери узнаваемости, что SmartHeart и сделали.

Как шаг к прогрессивности, SH придали фирменному зелёному цвету яркий неоновый оттенок. Хотели, чтобы человек, увидев в городе броский зелёный квадрат или рамку, идентифицировал их с 4D.

Команда клиента горела желанием внедрить новую концепцию и в пространство стройки, поэтому проработали и эту часть. Обычно в проектах эта задача ограничивается несколькими стандартными объектами — флаг, забор. Здесь же челлендж состоял в том, чтобы сделать строительный комплекс более универсальным, уникальным, интересным. Это огромная территория и, если она брендирована, она превращается в wow-объект и привлекает большой объем трафика.

К этому продукту (брендирование строительных площадок) можно подходить концептуально и индивидуально. Это очень крутая задача, за которую готова браться наша команда в проектах. Мы считаем, что это недооцененный объект, который многие застройщики не включают в пул задач по брендингу, а это must, один из самых ключевых элементов. Это всегда отличная история, когда брендинг пронизывает каждую точку касания как с покупателями, так и с сотрудниками компании.

Стас Окрух

Бренд-архитектура: процесс, интеллект, ценная работа

В портфеле 4D довольно большой пул объектов, каждый из которых имеет свою идентичность и стиль коммуникаций. Основная задача при работе с бренд-архитектурой была все упорядочить, систематизировать и обозначить принципы взаимодействия проектов с брендом девелопера. Это очень тонкий момент.

Клиент хотел, чтобы у объектов оставалось свое уникальное лицо. Здесь дизайнерам пришлось изрядно попотеть. Чтобы сохранить идентичность и одновременно показать принадлежность всех проектов к одному застройщику, понадобилось не только масштабировать дизайн-систему с зеленой рамкой и регламентировать ее использование в разных проектах, но и объединять шрифты, обосновывать использование определенного цветового диапазона — в общем, составлять очень объемные, четкие и структурные гайды.

Работа включала в себя множество технических тонкостей. Не потерять характер и объединить текущие и будущие проекты под одну стилистическую систему — не самая простая работа, где требуется высокая степень концентрации и внимательность к техническим тонкостям. Например, не смотря на ограниченную палитру неоновых оттенков, нам удалось создать систему подбора цветового кода и соответствующего фотостиля для будущих проектов. И мы гордимся результатом!

Женя Соломенцева

Коммуникационная стратегия: мы такие разные, но все-таки мы вместе

Регламентирование бренда 4D продолжилось работой над коммуникационной стратегией. Команда агентства решила, что объединение “дочек с мамой” должно осуществляться за счет применения смыслового образа. Его сердцем стала фраза “больше места для…”, окончание которой определяется в зависимости от основной ценности проекта, которую необходимо транслировать — “Больше места для меня”, “больше места для вдохновения” и т. д.

Подобная система делает коммуникацию застройщика, с одной стороны, достаточно единой: потребитель встречает на билбордах слово «больше» и понимает, что «больше»\“больше места” значит «4D». С другой стороны, коммуникация остается индивидуальной, потому что в сообщение «Больше места для …» можно добавить все, что угодно, в зависимости от целевой аудитории. И оно работает! Фактически SH создали коммуникационный гайд, который будет абсолютно понятен любому рекламному агентству, которое будет заниматься продвижением девелопера.

Результат превзошел изначальные ожидания, так как мы получили полноформатный универсальный метод по взаимодействию с брендом на всех этапах реализации проектов и в точках касания с ним. Все задачи, поставленные перед агентством, были максимально эффективно выполнены в процессе совместной поэтапной работы с командой компании 4D. Позиционирование бренда 4D в формате «Больше места» с первого раза вызвало в компании положительные впечатления, и мы единогласно приняли решение утвердить его. В дальнейшем трансформация этого позиционирования под проекты и другие структуры компании лишь подтвердила правильность выбора и его релевантность нашему видению. Мы видим в этом позиционирование большой потенциал для коммуникации и построения бренда вокруг него. Появилось понимание позиции бренда, голоса и его целей. Это позитивно повлияло на внутреннюю лояльность сотрудников к бренду, к его перспективам, развитию и амбициям.

Александр Дмитриев

ИТ-решения 4D — Rockwall | 4D IT Solutions

УСЛУГИ

Чем мы занимаемся

Дополнительная информация

• Проводите сеансы мозгового штурма для разработки потенциальных решений для бизнес-потребностей или проблем.
• Определите возможности для улучшения процесса.
• Подготовка и документирование требований к тестированию.
• Определите области, в которых ИТ может поддерживать потребности и цели бизнеса.
• Работать с бизнес-подразделениями над разработкой ИТ-стратегий и улучшением текущих внедрений ИТ.
• Создавайте и переносите программное обеспечение и службы в рамках всей организации.
• Работа с командами по продуктам и поставщикам для разработки масштабируемых решений и продуктов.
• Общайтесь и консультируйтесь с клиентами и внутренними заинтересованными сторонами для разработки соответствующих решений.

Дополнительная информация

Консультации по облачным технологиям, особенно по работе с компьютерными облачными системами. Они могут анализировать эти данные, чтобы определить, какое облачное решение лучше всего удовлетворит потребности клиента, чтобы они могли определить направление на основе своего анализа.

Компания разрабатывает действенную облачную стратегию и дорожную карту, обеспечивающую правильный баланс между эффективностью, инновациями и безопасностью. Cloud Consulting поможет вам понять, как облачные технологии и автоматизация могут помочь в достижении ваших бизнес-целей.

Подробнее

4D IT Solutions помогает реализовывать стратегические ИТ-инициативы, обеспечивающие инновации, гибкость и конкурентное преимущество. Мы помогаем вам реализовать критически важные бизнес-стратегии вашей организации с помощью наших решений для полного жизненного цикла и высококвалифицированных технических команд.

Отличие от 4D IT Solutions: После изучения и понимания того, как вы работаете с использованием ИТ, мы выявляем области неэффективности и области, в которых вы можете внести улучшения. Мы консультируемся с вашим исполнительным руководством и ИТ-директором, чтобы поделиться архитектурой ИТ-решений, планом для вашей высокоэффективной технической команды. Благодаря устранению слабых мест предыдущей системы такая технологическая трансформация обеспечивает новый уровень прибыльности и устойчивости, независимо от того, в какой отрасли вы работаете.

Подробнее о наших услугах

I

Да, благодаря индивидуальному командному взаимодействию мы стремимся понять ваши цели. Ваш новый план ИТ дополнит и ускорит реализацию ваших целей, бизнес-процессов и текущих возможностей информационных систем. По сути, мы становимся частью вашей команды с момента вашего официального обращения в 4D IT Solutions.

I

Ваша рентабельность увеличивается, поскольку мы СНИЖАЕМ ваши расходы на ИТ. Это достигается за счет предоставления четкого пути того, какие технологии следует внедрить и как максимизировать их функции.

I

Получите конкурентное преимущество следующего уровня благодаря тому же опыту и проверенному опыту, которым доверяют сотни других компаний, сотрудничая с 4D IT Solutions.

Представьте, что ваш бизнес — это лодка. Как и многие, независимо от того, хотите ли вы ехать быстро или медленно, на реактивном катере или в круизном стиле, каждый хотел бы также иметь плавную езду. Неправильный ИТ-план может выбить вас за борт. Правильный поможет вам насладиться поездкой в ​​горизонт.

ОТЗЫВЫ

Что говорят люди

Команда 4D IT без сомнения лучшая из всех, с кем мне приходилось работать. Отличное обслуживание клиентов и быстрое время отклика, а также! 4D IT управляет чрезвычайно тесным кораблем с хирургической точностью. Они сказали нам, что они архитекторы решений; что поначалу не имело для нас большого значения, пока мы не увидели, что это влечет за собой. Первоначально они встретились с нашим исполнительным руководством и ИТ-директором, стремясь узнать и понять, как мы работаем с использованием ИТ, и тем самым определили области неэффективности и то, что мы могли бы улучшить. Больше всего мне понравилось то, что в процессе изучения наших бизнес-процессов они определили в нашей серверной комнате несколько устройств, которые, по словам предыдущих ИТ-провайдеров, нам НЕОБХОДИМЫ, и заплатили за них огромные деньги. Сотрудники 4D IT смогли не только убрать это ненужное и дорогое сетевое/серверное оборудование, но и значительно сократить наши ежемесячные и квартальные накладные расходы на тысячи долларов.

Брайан Б.

С новыми правилами HIPAA Omnibus наш офис был в растерянности и очень запутался. 4D IT Solutions избавили нас от проблем с соблюдением требований HIPAA, решив и смягчив все проблемы, связанные с соответствием нашей сети и связанного с ней оборудования. Я был глубоко впечатлен их детальным пониманием и знанием HIPAA. Они не только привели нашу сеть в соответствие с требованиями, но и смогли провести успешную оценку рисков.

Доктор хиропрактики

Роли, Северная Каролина

Ваши услуги и опыт просто великолепны! Я работал со многими ИТ-группами, и я очень доволен вашей группой! Мы не смогли найти рентген; Технология 4D помогла парню из IDEXX найти его. Кроме того, мне не удалось выполнить поиск в Outlook, и ваша техника также устранила эту проблему.

Карен С.

Даллас, Техас, Ветеринарная клиника

Компания 4DIT Solutions превзошла ожидания моей компании в отношении ИТ-инфраструктуры. Пришел 4DIT, установил новые серверы, предложил невероятную индивидуальную архитектуру решения и говорил на языке, понятном всему моему персоналу. Обслуживание клиентов и время отклика феноменальны. Настоятельно рекомендую.

Люк Б.

ИТ-решения 4D — Rockwall | 4D IT Solutions

УСЛУГИ

Чем мы занимаемся

Дополнительная информация

• Проводите сеансы мозгового штурма для разработки потенциальных решений для бизнес-потребностей или проблем.
• Определите возможности для улучшения процесса.
• Подготовка и документирование требований к тестированию.
• Определите области, в которых ИТ может поддерживать потребности и цели бизнеса.
• Работать с бизнес-подразделениями над разработкой ИТ-стратегий и улучшением текущих внедрений ИТ.
• Создавайте и переносите программное обеспечение и службы в рамках всей организации.
• Работа с командами по продуктам и поставщикам для разработки масштабируемых решений и продуктов.
• Общайтесь и консультируйтесь с клиентами и внутренними заинтересованными сторонами для разработки соответствующих решений.

Дополнительная информация

Консультации по облачным технологиям, особенно по работе с компьютерными облачными системами. Они могут анализировать эти данные, чтобы определить, какое облачное решение лучше всего удовлетворит потребности клиента, чтобы они могли определить направление на основе своего анализа.

Компания разрабатывает действенную облачную стратегию и дорожную карту, обеспечивающую правильный баланс между эффективностью, инновациями и безопасностью. Cloud Consulting поможет вам понять, как облачные технологии и автоматизация могут помочь в достижении ваших бизнес-целей.

Подробнее

4D IT Solutions помогает реализовывать стратегические ИТ-инициативы, обеспечивающие инновации, гибкость и конкурентное преимущество. Мы помогаем вам реализовать критически важные бизнес-стратегии вашей организации с помощью наших решений для полного жизненного цикла и высококвалифицированных технических команд.

Отличие от 4D IT Solutions: После изучения и понимания того, как вы работаете с использованием ИТ, мы выявляем области неэффективности и области, в которых вы можете внести улучшения. Мы консультируемся с вашим исполнительным руководством и ИТ-директором, чтобы поделиться архитектурой ИТ-решений, планом для вашей высокоэффективной технической команды. Благодаря устранению слабых мест предыдущей системы такая технологическая трансформация обеспечивает новый уровень прибыльности и устойчивости, независимо от того, в какой отрасли вы работаете.

Подробнее о наших услугах

I

Да, благодаря индивидуальному командному взаимодействию мы стремимся понять ваши цели. Ваш новый план ИТ дополнит и ускорит реализацию ваших целей, бизнес-процессов и текущих возможностей информационных систем. По сути, мы становимся частью вашей команды с момента вашего официального обращения в 4D IT Solutions.

I

Ваша рентабельность увеличивается, поскольку мы СНИЖАЕМ ваши расходы на ИТ. Это достигается за счет предоставления четкого пути того, какие технологии следует внедрить и как максимизировать их функции.

I

Получите конкурентное преимущество следующего уровня благодаря тому же опыту и проверенному опыту, которым доверяют сотни других компаний, сотрудничая с 4D IT Solutions.

Представьте, что ваш бизнес — это лодка. Как и многие, независимо от того, хотите ли вы ехать быстро или медленно, на реактивном катере или в круизном стиле, каждый хотел бы также иметь плавную езду. Неправильный ИТ-план может выбить вас за борт. Правильный поможет вам насладиться поездкой в ​​горизонт.

ОТЗЫВЫ

Что говорят люди

Команда 4D IT без сомнения лучшая из всех, с кем мне приходилось работать. Отличное обслуживание клиентов и быстрое время отклика, а также! 4D IT управляет чрезвычайно тесным кораблем с хирургической точностью. Они сказали нам, что они архитекторы решений; что поначалу не имело для нас большого значения, пока мы не увидели, что это влечет за собой. Первоначально они встретились с нашим исполнительным руководством и ИТ-директором, стремясь узнать и понять, как мы работаем с использованием ИТ, и тем самым определили области неэффективности и то, что мы могли бы улучшить. Больше всего мне понравилось то, что в процессе изучения наших бизнес-процессов они определили в нашей серверной комнате несколько устройств, которые, по словам предыдущих ИТ-провайдеров, нам НЕОБХОДИМЫ, и заплатили за них огромные деньги. Сотрудники 4D IT смогли не только убрать это ненужное и дорогое сетевое/серверное оборудование, но и значительно сократить наши ежемесячные и квартальные накладные расходы на тысячи долларов.

Брайан Б.

С новыми правилами HIPAA Omnibus наш офис был в растерянности и очень запутался. 4D IT Solutions избавили нас от проблем с соблюдением требований HIPAA, решив и смягчив все проблемы, связанные с соответствием нашей сети и связанного с ней оборудования. Я был глубоко впечатлен их детальным пониманием и знанием HIPAA. Они не только привели нашу сеть в соответствие с требованиями, но и смогли провести успешную оценку рисков.

Доктор хиропрактики

Роли, Северная Каролина

Ваши услуги и опыт просто великолепны! Я работал со многими ИТ-группами, и я очень доволен вашей группой! Мы не смогли найти рентген; Технология 4D помогла парню из IDEXX найти его. Кроме того, мне не удалось выполнить поиск в Outlook, и ваша техника также устранила эту проблему.

Карен С.

Даллас, Техас, Ветеринарная клиника

Компания 4DIT Solutions превзошла ожидания моей компании в отношении ИТ-инфраструктуры. Пришел 4DIT, установил новые серверы, предложил невероятную индивидуальную архитектуру решения и говорил на языке, понятном всему моему персоналу. Обслуживание клиентов и время отклика феноменальны. Настоятельно рекомендую.

Люк Б.

ИТ-решения 4D — Rockwall | 4D IT Solutions

УСЛУГИ

Чем мы занимаемся

Дополнительная информация

• Проводите сеансы мозгового штурма для разработки потенциальных решений для бизнес-потребностей или проблем.
• Определите возможности для улучшения процесса.
• Подготовка и документирование требований к тестированию.
• Определите области, в которых ИТ может поддерживать потребности и цели бизнеса.
• Работать с бизнес-подразделениями над разработкой ИТ-стратегий и улучшением текущих внедрений ИТ.
• Создавайте и переносите программное обеспечение и службы в рамках всей организации.
• Работа с командами по продуктам и поставщикам для разработки масштабируемых решений и продуктов.
• Общайтесь и консультируйтесь с клиентами и внутренними заинтересованными сторонами для разработки соответствующих решений.

Дополнительная информация

Консультации по облачным технологиям, особенно по работе с компьютерными облачными системами. Они могут анализировать эти данные, чтобы определить, какое облачное решение лучше всего удовлетворит потребности клиента, чтобы они могли определить направление на основе своего анализа.

Компания разрабатывает действенную облачную стратегию и дорожную карту, обеспечивающую правильный баланс между эффективностью, инновациями и безопасностью. Cloud Consulting поможет вам понять, как облачные технологии и автоматизация могут помочь в достижении ваших бизнес-целей.

Подробнее

4D IT Solutions помогает реализовывать стратегические ИТ-инициативы, обеспечивающие инновации, гибкость и конкурентное преимущество. Мы помогаем вам реализовать критически важные бизнес-стратегии вашей организации с помощью наших решений для полного жизненного цикла и высококвалифицированных технических команд.

Отличие от 4D IT Solutions: После изучения и понимания того, как вы работаете с использованием ИТ, мы выявляем области неэффективности и области, в которых вы можете внести улучшения. Мы консультируемся с вашим исполнительным руководством и ИТ-директором, чтобы поделиться архитектурой ИТ-решений, планом для вашей высокоэффективной технической команды. Благодаря устранению слабых мест предыдущей системы такая технологическая трансформация обеспечивает новый уровень прибыльности и устойчивости, независимо от того, в какой отрасли вы работаете.

Подробнее о наших услугах

I

Да, благодаря индивидуальному командному взаимодействию мы стремимся понять ваши цели. Ваш новый план ИТ дополнит и ускорит реализацию ваших целей, бизнес-процессов и текущих возможностей информационных систем. По сути, мы становимся частью вашей команды с момента вашего официального обращения в 4D IT Solutions.

I

Ваша рентабельность увеличивается, поскольку мы СНИЖАЕМ ваши расходы на ИТ. Это достигается за счет предоставления четкого пути того, какие технологии следует внедрить и как максимизировать их функции.

I

Получите конкурентное преимущество следующего уровня благодаря тому же опыту и проверенному опыту, которым доверяют сотни других компаний, сотрудничая с 4D IT Solutions.

Представьте, что ваш бизнес — это лодка. Как и многие, независимо от того, хотите ли вы ехать быстро или медленно, на реактивном катере или в круизном стиле, каждый хотел бы также иметь плавную езду. Неправильный ИТ-план может выбить вас за борт. Правильный поможет вам насладиться поездкой в ​​горизонт.

ОТЗЫВЫ

Что говорят люди

Команда 4D IT без сомнения лучшая из всех, с кем мне приходилось работать. Отличное обслуживание клиентов и быстрое время отклика, а также! 4D IT управляет чрезвычайно тесным кораблем с хирургической точностью. Они сказали нам, что они архитекторы решений; что поначалу не имело для нас большого значения, пока мы не увидели, что это влечет за собой. Первоначально они встретились с нашим исполнительным руководством и ИТ-директором, стремясь узнать и понять, как мы работаем с использованием ИТ, и тем самым определили области неэффективности и то, что мы могли бы улучшить. Больше всего мне понравилось то, что в процессе изучения наших бизнес-процессов они определили в нашей серверной комнате несколько устройств, которые, по словам предыдущих ИТ-провайдеров, нам НЕОБХОДИМЫ, и заплатили за них огромные деньги. Сотрудники 4D IT смогли не только убрать это ненужное и дорогое сетевое/серверное оборудование, но и значительно сократить наши ежемесячные и квартальные накладные расходы на тысячи долларов.

Брайан Б.

С новыми правилами HIPAA Omnibus наш офис был в растерянности и очень запутался. 4D IT Solutions избавили нас от проблем с соблюдением требований HIPAA, решив и смягчив все проблемы, связанные с соответствием нашей сети и связанного с ней оборудования. Я был глубоко впечатлен их детальным пониманием и знанием HIPAA. Они не только привели нашу сеть в соответствие с требованиями, но и смогли провести успешную оценку рисков.

Доктор хиропрактики

Роли, Северная Каролина

Ваши услуги и опыт просто великолепны! Я работал со многими ИТ-группами, и я очень доволен вашей группой! Мы не смогли найти рентген; Технология 4D помогла парню из IDEXX найти его. Кроме того, мне не удалось выполнить поиск в Outlook, и ваша техника также устранила эту проблему.

Карен С.

Даллас, Техас, Ветеринарная клиника

Компания 4DIT Solutions превзошла ожидания моей компании в отношении ИТ-инфраструктуры. Пришел 4DIT, установил новые серверы, предложил невероятную индивидуальную архитектуру решения и говорил на языке, понятном всему моему персоналу. Обслуживание клиентов и время отклика феноменальны. Настоятельно рекомендую.

Люк Б.

ИТ-решения 4D — Rockwall | 4D IT Solutions

УСЛУГИ

Чем мы занимаемся

Дополнительная информация

• Проводите сеансы мозгового штурма для разработки потенциальных решений для бизнес-потребностей или проблем.
• Определите возможности для улучшения процесса.
• Подготовка и документирование требований к тестированию.
• Определите области, в которых ИТ может поддерживать потребности и цели бизнеса.
• Работать с бизнес-подразделениями над разработкой ИТ-стратегий и улучшением текущих внедрений ИТ.
• Создавайте и переносите программное обеспечение и службы в рамках всей организации.
• Работа с командами по продуктам и поставщикам для разработки масштабируемых решений и продуктов.
• Общайтесь и консультируйтесь с клиентами и внутренними заинтересованными сторонами для разработки соответствующих решений.

Дополнительная информация

Консультации по облачным технологиям, особенно по работе с компьютерными облачными системами. Они могут анализировать эти данные, чтобы определить, какое облачное решение лучше всего удовлетворит потребности клиента, чтобы они могли определить направление на основе своего анализа.

Компания разрабатывает действенную облачную стратегию и дорожную карту, обеспечивающую правильный баланс между эффективностью, инновациями и безопасностью. Cloud Consulting поможет вам понять, как облачные технологии и автоматизация могут помочь в достижении ваших бизнес-целей.

Подробнее

4D IT Solutions помогает реализовывать стратегические ИТ-инициативы, обеспечивающие инновации, гибкость и конкурентное преимущество. Мы помогаем вам реализовать критически важные бизнес-стратегии вашей организации с помощью наших решений для полного жизненного цикла и высококвалифицированных технических команд.

Отличие от 4D IT Solutions: После изучения и понимания того, как вы работаете с использованием ИТ, мы выявляем области неэффективности и области, в которых вы можете внести улучшения. Мы консультируемся с вашим исполнительным руководством и ИТ-директором, чтобы поделиться архитектурой ИТ-решений, планом для вашей высокоэффективной технической команды. Благодаря устранению слабых мест предыдущей системы такая технологическая трансформация обеспечивает новый уровень прибыльности и устойчивости, независимо от того, в какой отрасли вы работаете.

Подробнее о наших услугах

I

Да, благодаря индивидуальному командному взаимодействию мы стремимся понять ваши цели. Ваш новый план ИТ дополнит и ускорит реализацию ваших целей, бизнес-процессов и текущих возможностей информационных систем. По сути, мы становимся частью вашей команды с момента вашего официального обращения в 4D IT Solutions.

I

Ваша рентабельность увеличивается, поскольку мы СНИЖАЕМ ваши расходы на ИТ. Это достигается за счет предоставления четкого пути того, какие технологии следует внедрить и как максимизировать их функции.

I

Получите конкурентное преимущество следующего уровня благодаря тому же опыту и проверенному опыту, которым доверяют сотни других компаний, сотрудничая с 4D IT Solutions.

Представьте, что ваш бизнес — это лодка. Как и многие, независимо от того, хотите ли вы ехать быстро или медленно, на реактивном катере или в круизном стиле, каждый хотел бы также иметь плавную езду. Неправильный ИТ-план может выбить вас за борт. Правильный поможет вам насладиться поездкой в ​​горизонт.

ОТЗЫВЫ

Что говорят люди

Команда 4D IT без сомнения лучшая из всех, с кем мне приходилось работать. Отличное обслуживание клиентов и быстрое время отклика, а также! 4D IT управляет чрезвычайно тесным кораблем с хирургической точностью. Они сказали нам, что они архитекторы решений; что поначалу не имело для нас большого значения, пока мы не увидели, что это влечет за собой. Первоначально они встретились с нашим исполнительным руководством и ИТ-директором, стремясь узнать и понять, как мы работаем с использованием ИТ, и тем самым определили области неэффективности и то, что мы могли бы улучшить. Больше всего мне понравилось то, что в процессе изучения наших бизнес-процессов они определили в нашей серверной комнате несколько устройств, которые, по словам предыдущих ИТ-провайдеров, нам НЕОБХОДИМЫ, и заплатили за них огромные деньги. Сотрудники 4D IT смогли не только убрать это ненужное и дорогое сетевое/серверное оборудование, но и значительно сократить наши ежемесячные и квартальные накладные расходы на тысячи долларов.

Брайан Б.

С новыми правилами HIPAA Omnibus наш офис был в растерянности и очень запутался. 4D IT Solutions избавили нас от проблем с соблюдением требований HIPAA, решив и смягчив все проблемы, связанные с соответствием нашей сети и связанного с ней оборудования. Я был глубоко впечатлен их детальным пониманием и знанием HIPAA. Они не только привели нашу сеть в соответствие с требованиями, но и смогли провести успешную оценку рисков.

Доктор хиропрактики

Роли, Северная Каролина

Ваши услуги и опыт просто великолепны! Я работал со многими ИТ-группами, и я очень доволен вашей группой! Мы не смогли найти рентген; Технология 4D помогла парню из IDEXX найти его. Кроме того, мне не удалось выполнить поиск в Outlook, и ваша техника также устранила эту проблему.

Карен С.

Даллас, Техас, Ветеринарная клиника

Компания 4DIT Solutions превзошла ожидания моей компании в отношении ИТ-инфраструктуры. Пришел 4DIT, установил новые серверы, предложил невероятную индивидуальную архитектуру решения и говорил на языке, понятном всему моему персоналу. Обслуживание клиентов и время отклика феноменальны. Настоятельно рекомендую.

Люк Б.

ИТ-решения 4D — Rockwall | 4D IT Solutions

УСЛУГИ

Чем мы занимаемся

Дополнительная информация

• Проводите сеансы мозгового штурма для разработки потенциальных решений для бизнес-потребностей или проблем.
• Определите возможности для улучшения процесса.
• Подготовка и документирование требований к тестированию.
• Определите области, в которых ИТ может поддерживать потребности и цели бизнеса.
• Работать с бизнес-подразделениями над разработкой ИТ-стратегий и улучшением текущих внедрений ИТ.
• Создавайте и переносите программное обеспечение и службы в рамках всей организации.
• Работа с командами по продуктам и поставщикам для разработки масштабируемых решений и продуктов.
• Общайтесь и консультируйтесь с клиентами и внутренними заинтересованными сторонами для разработки соответствующих решений.

Дополнительная информация

Консультации по облачным технологиям, особенно по работе с компьютерными облачными системами. Они могут анализировать эти данные, чтобы определить, какое облачное решение лучше всего удовлетворит потребности клиента, чтобы они могли определить направление на основе своего анализа.

Компания разрабатывает действенную облачную стратегию и дорожную карту, обеспечивающую правильный баланс между эффективностью, инновациями и безопасностью. Cloud Consulting поможет вам понять, как облачные технологии и автоматизация могут помочь в достижении ваших бизнес-целей.

Подробнее

4D IT Solutions помогает реализовывать стратегические ИТ-инициативы, обеспечивающие инновации, гибкость и конкурентное преимущество. Мы помогаем вам реализовать критически важные бизнес-стратегии вашей организации с помощью наших решений для полного жизненного цикла и высококвалифицированных технических команд.

Отличие от 4D IT Solutions: После изучения и понимания того, как вы работаете с использованием ИТ, мы выявляем области неэффективности и области, в которых вы можете внести улучшения. Мы консультируемся с вашим исполнительным руководством и ИТ-директором, чтобы поделиться архитектурой ИТ-решений, планом для вашей высокоэффективной технической команды. Благодаря устранению слабых мест предыдущей системы такая технологическая трансформация обеспечивает новый уровень прибыльности и устойчивости, независимо от того, в какой отрасли вы работаете.

Подробнее о наших услугах

I

Да, благодаря индивидуальному командному взаимодействию мы стремимся понять ваши цели. Ваш новый план ИТ дополнит и ускорит реализацию ваших целей, бизнес-процессов и текущих возможностей информационных систем. По сути, мы становимся частью вашей команды с момента вашего официального обращения в 4D IT Solutions.

I

Ваша рентабельность увеличивается, поскольку мы СНИЖАЕМ ваши расходы на ИТ. Это достигается за счет предоставления четкого пути того, какие технологии следует внедрить и как максимизировать их функции.

I

Получите конкурентное преимущество следующего уровня благодаря тому же опыту и проверенному опыту, которым доверяют сотни других компаний, сотрудничая с 4D IT Solutions.

Представьте, что ваш бизнес — это лодка. Как и многие, независимо от того, хотите ли вы ехать быстро или медленно, на реактивном катере или в круизном стиле, каждый хотел бы также иметь плавную езду. Неправильный ИТ-план может выбить вас за борт. Правильный поможет вам насладиться поездкой в ​​горизонт.

ОТЗЫВЫ

Что говорят люди

Команда 4D IT без сомнения лучшая из всех, с кем мне приходилось работать. Отличное обслуживание клиентов и быстрое время отклика, а также! 4D IT управляет чрезвычайно тесным кораблем с хирургической точностью. Они сказали нам, что они архитекторы решений; что поначалу не имело для нас большого значения, пока мы не увидели, что это влечет за собой. Первоначально они встретились с нашим исполнительным руководством и ИТ-директором, стремясь узнать и понять, как мы работаем с использованием ИТ, и тем самым определили области неэффективности и то, что мы могли бы улучшить. Больше всего мне понравилось то, что в процессе изучения наших бизнес-процессов они определили в нашей серверной комнате несколько устройств, которые, по словам предыдущих ИТ-провайдеров, нам НЕОБХОДИМЫ, и заплатили за них огромные деньги. Сотрудники 4D IT смогли не только убрать это ненужное и дорогое сетевое/серверное оборудование, но и значительно сократить наши ежемесячные и квартальные накладные расходы на тысячи долларов.

Брайан Б.

С новыми правилами HIPAA Omnibus наш офис был в растерянности и очень запутался. 4D IT Solutions избавили нас от проблем с соблюдением требований HIPAA, решив и смягчив все проблемы, связанные с соответствием нашей сети и связанного с ней оборудования. Я был глубоко впечатлен их детальным пониманием и знанием HIPAA. Они не только привели нашу сеть в соответствие с требованиями, но и смогли провести успешную оценку рисков.

Доктор хиропрактики

Роли, Северная Каролина

Ваши услуги и опыт просто великолепны! Я работал со многими ИТ-группами, и я очень доволен вашей группой! Мы не смогли найти рентген; Технология 4D помогла парню из IDEXX найти его. Кроме того, мне не удалось выполнить поиск в Outlook, и ваша техника также устранила эту проблему.

Карен С.

Даллас, Техас, Ветеринарная клиника

Компания 4DIT Solutions превзошла ожидания моей компании в отношении ИТ-инфраструктуры. Пришел 4DIT, установил новые серверы, предложил невероятную индивидуальную архитектуру решения и говорил на языке, понятном всему моему персоналу. Обслуживание клиентов и время отклика феноменальны. Настоятельно рекомендую.

Люк Б.

ИТ-решения 4D — Rockwall | 4D IT Solutions

УСЛУГИ

Чем мы занимаемся

Дополнительная информация

• Проводите сеансы мозгового штурма для разработки потенциальных решений для бизнес-потребностей или проблем.
• Определите возможности для улучшения процесса.
• Подготовка и документирование требований к тестированию.
• Определите области, в которых ИТ может поддерживать потребности и цели бизнеса.
• Работать с бизнес-подразделениями над разработкой ИТ-стратегий и улучшением текущих внедрений ИТ.
• Создавайте и переносите программное обеспечение и службы в рамках всей организации.
• Работа с командами по продуктам и поставщикам для разработки масштабируемых решений и продуктов.
• Общайтесь и консультируйтесь с клиентами и внутренними заинтересованными сторонами для разработки соответствующих решений.

Дополнительная информация

Консультации по облачным технологиям, особенно по работе с компьютерными облачными системами. Они могут анализировать эти данные, чтобы определить, какое облачное решение лучше всего удовлетворит потребности клиента, чтобы они могли определить направление на основе своего анализа.

Компания разрабатывает действенную облачную стратегию и дорожную карту, обеспечивающую правильный баланс между эффективностью, инновациями и безопасностью. Cloud Consulting поможет вам понять, как облачные технологии и автоматизация могут помочь в достижении ваших бизнес-целей.

Подробнее

4D IT Solutions помогает реализовывать стратегические ИТ-инициативы, обеспечивающие инновации, гибкость и конкурентное преимущество. Мы помогаем вам реализовать критически важные бизнес-стратегии вашей организации с помощью наших решений для полного жизненного цикла и высококвалифицированных технических команд.

Отличие от 4D IT Solutions: После изучения и понимания того, как вы работаете с использованием ИТ, мы выявляем области неэффективности и области, в которых вы можете внести улучшения. Мы консультируемся с вашим исполнительным руководством и ИТ-директором, чтобы поделиться архитектурой ИТ-решений, планом для вашей высокоэффективной технической команды. Благодаря устранению слабых мест предыдущей системы такая технологическая трансформация обеспечивает новый уровень прибыльности и устойчивости, независимо от того, в какой отрасли вы работаете.

Подробнее о наших услугах

I

Да, благодаря индивидуальному командному взаимодействию мы стремимся понять ваши цели. Ваш новый план ИТ дополнит и ускорит реализацию ваших целей, бизнес-процессов и текущих возможностей информационных систем. По сути, мы становимся частью вашей команды с момента вашего официального обращения в 4D IT Solutions.

I

Ваша рентабельность увеличивается, поскольку мы СНИЖАЕМ ваши расходы на ИТ. Это достигается за счет предоставления четкого пути того, какие технологии следует внедрить и как максимизировать их функции.

I

Получите конкурентное преимущество следующего уровня благодаря тому же опыту и проверенному опыту, которым доверяют сотни других компаний, сотрудничая с 4D IT Solutions.

Представьте, что ваш бизнес — это лодка. Как и многие, независимо от того, хотите ли вы ехать быстро или медленно, на реактивном катере или в круизном стиле, каждый хотел бы также иметь плавную езду. Неправильный ИТ-план может выбить вас за борт. Правильный поможет вам насладиться поездкой в ​​горизонт.

ОТЗЫВЫ

Что говорят люди

Команда 4D IT без сомнения лучшая из всех, с кем мне приходилось работать. Отличное обслуживание клиентов и быстрое время отклика, а также! 4D IT управляет чрезвычайно тесным кораблем с хирургической точностью. Они сказали нам, что они архитекторы решений; что поначалу не имело для нас большого значения, пока мы не увидели, что это влечет за собой. Первоначально они встретились с нашим исполнительным руководством и ИТ-директором, стремясь узнать и понять, как мы работаем с использованием ИТ, и тем самым определили области неэффективности и то, что мы могли бы улучшить. Больше всего мне понравилось то, что в процессе изучения наших бизнес-процессов они определили в нашей серверной комнате несколько устройств, которые, по словам предыдущих ИТ-провайдеров, нам НЕОБХОДИМЫ, и заплатили за них огромные деньги. Сотрудники 4D IT смогли не только убрать это ненужное и дорогое сетевое/серверное оборудование, но и значительно сократить наши ежемесячные и квартальные накладные расходы на тысячи долларов.

Брайан Б.

С новыми правилами HIPAA Omnibus наш офис был в растерянности и очень запутался. 4D IT Solutions избавили нас от проблем с соблюдением требований HIPAA, решив и смягчив все проблемы, связанные с соответствием нашей сети и связанного с ней оборудования. Я был глубоко впечатлен их детальным пониманием и знанием HIPAA. Они не только привели нашу сеть в соответствие с требованиями, но и смогли провести успешную оценку рисков.

Доктор хиропрактики

Роли, Северная Каролина

Ваши услуги и опыт просто великолепны! Я работал со многими ИТ-группами, и я очень доволен вашей группой! Мы не смогли найти рентген; Технология 4D помогла парню из IDEXX найти его. Кроме того, мне не удалось выполнить поиск в Outlook, и ваша техника также устранила эту проблему.