Рис 5: Эллипс и его директрисы.
 
Опишем сначала элементарные свойства эллипса, следующие непосредственно из канонического уравнения (19).
1. Из этого уравнения следует, что если точка $(x,y)$ принадлежит эллипсу, то выполняются неравенства $|x| \leq a $, $|y| \leq b$. Таким образом, все точки эллипса лежат в этом прямоугольнике (конечном!).
2. Так как переменные $x,y$ входят в уравнение эллипса только в квадратах, то из того, что $(x,y)$ лежат на эллипсе следует, что точки $(\pm x, \, \pm y)$ также лежат на эллипсе при любом выборе знаков. Это означает, что эллипс симметричен при отражении относительной осей координат и имеет центр симметрии, точку $O$.
 
3.4 Прямая на плоскости 3.6 Гипербола
 
В.А. Ильин, Э.Г. Позняк — Аналитическая геометрия (7-е издание) — DJVU, страница 32
DJVU-файл из архива «В.А. Ильин, Э.Г. Позняк — Аналитическая геометрия (7-е издание)», который расположен в категории «». Всё это находится в предмете «линейная алгебра и аналитическая геометрия» из раздела «», которые можно найти в файловом архиве МГУ им. Ломоносова. Не смотря на прямую связь этого архива с МГУ им. Ломоносова, его также можно найти и в других разделах. .
Обращаясь к уравнению (6.9), мы видим, что при указанных условиях это уравнение эквивалентно соотношению х у =Ь ~ —,-1. (6.17) Иными словами, рассматриваемая часть гиперболы представляет собой график функции (6.! 7) ‘), Легко убедиться, что эта функция мо- жет быть представлена в следующей форме: Ь Ь у= — х— х + тГхз — аз (6.
рассмотрим разность )’ — у (рис. 6.7 а). Используя соотношения (6.18) и (6.19), получим Ь (6.20) — у— х ж чГх — а ‘) Абсциссы х точек 02 нс равны нулю ) В силу свойства й’ гиперболы (6.9) абсциссы ее точек уловлетворяют условию )х ! > а Для точек первои четверти зто условие к2олсет быть записана в виде х > и. ‘|) По поводу понятия график функции сы вып 1, гл 1, Э 2, и 4 ь ь делаются уравнениями у = — х и у = — — х, то координаты х и у точек а а 62 в силу их расположения удовлетворяют неравенству Ь,га < ~ у ~ у’ ) х ~ ).
Из этого неравенства вытекает неравенство ) х ~ )2а < )у!)г Ь, из которого х у в свою очередь следуют неравенства — „— —, < О < 1, а так как для точек а Ь 1гл б 154 ЛИ1ШИ ВТОРОГО ПОРЯДКА Из соотношения (6. 20) следует, что при х — э 0 разность У вЂ” у стремится к нулю. Абсолютная величина ) У вЂ” у( равна длине отрезка МАГ(рис. 6 7 а).
20) следует, что при х — э 0 разность У вЂ” у стремится к нулю. Абсолютная величина ) У вЂ” у( равна длине отрезка МАГ(рис. 6 7 а).
Так как расстояние МР от точки М гиперболы до рассматриваемой диагонали не превышает длины отрезка МАГ, то при удалении точки М гипербольг в бесконечность (т.е. при х — + О) расстояние МР стремится к нулю. Следовательно, рассматриваемая часть ветви гиперболы приближается к соответствующей диагонали прямоугольника О. В силу симметрии аналогичным свойством обладают и другие части гиперболы, расположенные во второй, третьей и четвертой четвертях. Рис. 6 7 Диагонали прямоугольника В обычно называются асимптотами гиперболы. Отметим, что асимптоты гиперболы определяются уравнениями Ь Ь у= — х и у= — — х.
(6.21) а а 4′. Наряду с гиперболой (6.9) рассматривают так называемую сопряженную по отноидению к ней гиперболу. Сопряженная гипербола определяется каноническим уравнением (6.22) На рис.6.7 б изображены гипербола (6.9) и сопряженная ей гипербола (6,22).
Очевидно, что сопряженная гипербола имеет те же асимптоты, что и данная. Иными словами, асимптоты сопряженной гиперболы определяются уравнениями (6.21). Заметим, что гипербола (6.9) в свою очередь является сопряженной по отношению к гиперболе (6.22).
‘) Чтобы убедиться, что уравнение 16 22) определяет гиперболу, достаточно положить х = Р, у = х и уииожить обе части етого уравнении па — 1. ДИРЕКТРИСЫ ЭЛЛИПСА, ГИНЕРЬОЛЫ И ПАРАБОЛЫ у 3! 3. Исследование формы параболы. Обратимся к каноническому уравнению параболы (6.15): у = 2рх. (6. 15) 1’. Парабола имеет ось симметрии (ось параболы).
Точка пересечения параболы с осью называется вершинои параболы. Действительно, в уравнении (6.15) величина у фигурирует вчетной степени. Следовательно, если х , М(х, координаты х и у точки М удовлетворяют уравнению (6.15) (т.е. точка М располагается на параболе), то этому уравнению удовлетворяют координаты (х, — у) симметричной ей точки относительно оси Ох (рис.
6.8). Таким образом, если парабола задана своим каноническим уравнением (6. 15), то осью этой параболь! является Р’т ось Ох. Очевидно, вершиной параболы является начало координат. 2′. Вся парабола расположена в правой полуплоскости плоскости Оху. В самом деле, так как р > О, то уравнению (6.15) удовлетворяют координаты точек лишь с неотрицательными абсциссами. Такие точки располагаются в правой полуплоскости. 3′.
15), то осью этой параболь! является Р’т ось Ох. Очевидно, вершиной параболы является начало координат. 2′. Вся парабола расположена в правой полуплоскости плоскости Оху. В самом деле, так как р > О, то уравнению (6.15) удовлетворяют координаты точек лишь с неотрицательными абсциссами. Такие точки располагаются в правой полуплоскости. 3′.
Из рассуждений п. 3 ~ 1 этой главы вытекает, что директриса параболы, определяемой каноническим уравнением (6.15), имеет уравнение у) у = — р!!2 й 3. Директрисы эллипса, гиперболы и параболы Определение параболы, данное в п. 3 ~ 1 этой главы, базировалось на свойстве этой кривой, которое связано с ее фокусом и директрисой. (6.23) 4′. Любые две параболы подобны друг другу. Пусть уа = 2рх и у = 2р*х — канонические уравнения этих парабол в декартовой системе Оху; у = йх — уравнение произвольной прямой, проходящей через О, а (х, у) и (х», у*) — координаты точек пересечения этой прямой с параболами.
Используя канонические уравнения, получим х = 2р/йз, у = ч. 2р/й, хл = 2р»‘/й, у’ =ч.2р'»г!й. Из последних формул вытекает, что — = р/р», — = р!!р*. Но эти равенства означают подобие рассматри- Х ваемых парабол относительно точки О. 5′. Отметим, что кривая у’ = 2рх при р < О также является параболой, которая целиком располагается в левой полуплоскости плоскости Оху. Чтобы убедиться в этом, достаточно заменить х на -х и -р на р.
2р/й, хл = 2р»‘/й, у’ =ч.2р'»г!й. Из последних формул вытекает, что — = р/р», — = р!!р*. Но эти равенства означают подобие рассматри- Х ваемых парабол относительно точки О. 5′. Отметим, что кривая у’ = 2рх при р < О также является параболой, которая целиком располагается в левой полуплоскости плоскости Оху. Чтобы убедиться в этом, достаточно заменить х на -х и -р на р.
ЛИ1ШИ ВТОРОГО ПОРЯДКА 1гл б 156 Это свойство можно сформулировать также и следующим образом: парабола есть геометрическое место точек плоскости, для которых отношение расстояния до фокуса к рассптоянию до отвечающей этому фокусу директрисы есть величина постоянная, равная единице. Оказывается, отличный от окружности эллипс и гипербола обладают аналогичным свойством: для каждого фокуса ‘) эллипса или гиперболья можно указать такую прямую, называемую д ир е к т р ис о и, что отношение расстояния от точек этих кривых до фокуса к расстоянию до отвечающей этому фокусу директрисы есть величина постоянная. Данный параграф посвящен выяснению этого свойства эллипса и гиперболы.
1. Эксцентриситет эллипса и гиперболы. Обратимся к эллипсу (гиперболе). Пусть с — половина расстояния между фокусами эллипса )(гиперболы), а — большая полуось эллипса (действительная полуось гиперболы). Определение. 3 к сцен т р и си тетом эллипса (гипербольг) называется величина е, равная отношению с)а: е = с,Га.
(6.24) 3 а м е ч а н и е 1. Учитывая связь величины с с длинами а и Ь большой и малой полуосей эллипса (с длинами действительной и мнимой полуосей гиперболы) (см. формулы (6 5) и (6.! О)), легко получить следующие выражения для эксцентриситета е: Г Ь для эллипса е = ~1- —,, а (6.25) Г ь’ для гиперболы е = ~1е —, а (6.25′) ) Напомним, что отличный от окружности эллипс и гипсроола имеют по два фокуса аэ ) Голи эллипс представляет собои окружность, то с = О. й Напомним, что величина Ь как для эллипса, так и для гиперболы не равна нулю Из формул (6.25) и (6.25′) вытекает, что эксцентриситет эллипса меньше единицы, а эксцентриситет гипербольг больше единицы а), Отметим, что эксцентриситет окружности равен нулю (для окружности Ь = а).
3 а м е ч а н и е 2. Два эллипса (две гиперболы), имеющих одинаковый эксцентриситет, подобны. В самом деле, из формулы (6.25) для эксцентриситета эллипса (из формулы (6.25′) для зксцентриситета гиперболы) вытекает, что эллипсы с одинаковым эксцентриситетом имеют одинаковое отношение Ь,Га малой и большой полуосей (гиперболы с 157 ДИРЕКТРИСЫ ЗЛЛИПСА, ГИПЕРБОЛЫ И ПАРАБОЛЫ У 31 одинаковым зксцентриситетом имеют одинаковое отношение Ь,га мнимой и действительной полуосей).
Такие эллипсы (гиперболы) подобны ‘). 3 а м е ч а н и е 3. Эксцентриситет эллипса можно рассматривать как меру его «вытянутости » : чем больше эксцентриситет е (см. формулу 16.25)), тем меньше отношение Ьуа малой полуоси эллипса Ь к его большой полуоси а. На рис. 6.9 изображены эллипсы с разными эксцентриситетами, но с одинаковой большой полуосью а.
3 а м е ч а н и е 4. Эксцентриситет гиперболы можно рассматривать как числовую характеристику величины раствора угла между ее асимптотами. В самом деле, отношение Ьуа равно тангенсу половины угла между асимптотами гиперболы. 2. Директрисы эллипса и гиперболы. 1′. Директрисьг эллипса. Мы выяснили, что любой, отличный от окружности эллипс имеет большую и малую оси и центр — точку пересечения этих осей (см. п. 1 ~ 2 этой главы). Обозначим через с половину расстояния между фокусами с»г и сг эллипса, через а его большую полуось и через О его центр (рис.
2. Директрисы эллипса и гиперболы. 1′. Директрисьг эллипса. Мы выяснили, что любой, отличный от окружности эллипс имеет большую и малую оси и центр — точку пересечения этих осей (см. п. 1 ~ 2 этой главы). Обозначим через с половину расстояния между фокусами с»г и сг эллипса, через а его большую полуось и через О его центр (рис.
6.!О). с=о Рис. Б.10 Рис 69 Пусть е — эксцентриситет этого эллипса (так как эллипс отличен от окружности, то е м О) и л — плоскость, в которой расположен эллипс. Малая ось эллипса разбивает эту плоскость на две полуплоскости. Обозначим через ~, (г = 1, 2) ту из этих полуплоскостей, в которой лежит фокус г» г (г = 1, 2). Определение. Д и р е к т р и с о й О, 11’= 1, 2) эллипса, отвечающей фокусу сг 1)= 1, 2), назьгвается прямая, расположенная в полуплоскости и, (г’ = 1, 2) перпендикулярно большой оси эллипса на расстоянии а/е от его центра.
3 а м е ч а н и е 1. Выберем начало декартовой прямоугольной системы координат в середине отрезка г» гсд, а оси Ох и Оу направим так, ‘) Чтобы убедиться в атом, лостато*шо расположить тти аллнпсы 1соответственно гиперболы) так. чтобы их пентры н одноименные главные оси совпадали Тогда иа канонических уравнении легко следует подобие кривых с равными отношениями Ь)а. линии ВТОРОГО ИОРядкА ~ГЛ 6 уравнение директрисы О,: х = -а?е, уравнение директрисы 1лз. .х = атге. (6.26) 3 а м е ч а н и е 2. Директрисы эллипса расположены вне эллипса.
чтобы их пентры н одноименные главные оси совпадали Тогда иа канонических уравнении легко следует подобие кривых с равными отношениями Ь)а. линии ВТОРОГО ИОРядкА ~ГЛ 6 уравнение директрисы О,: х = -а?е, уравнение директрисы 1лз. .х = атге. (6.26) 3 а м е ч а н и е 2. Директрисы эллипса расположены вне эллипса.
Действительно, эллипс расположен в прямоугольнике )х( < а,)у) < Ь (см. п. 1 ~ 2 этой главы и рис. 6.4), стороны которого перпендикулярны большой и малой осям эллипса. Из определения директрис вытекает, что они параллельны двум перпендикулярным большой оси эллипса сторонам этого прямоугольника. Поскольку упомянутые стороны отстоят от центра эллипса на расстоянии а, а директрисы — на расстоянии а?е > а (О < е < 1), то директрисы расположены вне прямоугольника, а следовательно, и вне эллипса. 3 а м е ч а н и е 3.
Мы только что выяснили, что директрисы расположены вне эллипса. Отсюда вытекает, что точки эллипса и его центр расположены по одну сторону от каждой из его директрис. 3 а м е ч а н и е 4. Обозначим через р расстояние от фокуса эллипса до соответствующей этому фокусу директрисы. Поскольку расстояние от центра эллипса до директрисы равно а)е, а расстояние от центра зла липса до фокуса равно с, то р равно — — с ). Так как с = ае, то для р е получаем следующее выражение: р=а — — е =а (6.2?) Докажем теорему, выясняющую важное свойство отличного от окружности эллипса и его директрис. Теорема 6.1. Отношение расстояния г, от точки М эллипса до фокуса с, к расстоянию й, от этой точки до отвечающей этому фокусу директрисьг 1), равно эксцентриситету е этого эллипса.
3 а м е ч а н и е 4. Обозначим через р расстояние от фокуса эллипса до соответствующей этому фокусу директрисы. Поскольку расстояние от центра эллипса до директрисы равно а)е, а расстояние от центра зла липса до фокуса равно с, то р равно — — с ). Так как с = ае, то для р е получаем следующее выражение: р=а — — е =а (6.2?) Докажем теорему, выясняющую важное свойство отличного от окружности эллипса и его директрис. Теорема 6.1. Отношение расстояния г, от точки М эллипса до фокуса с, к расстоянию й, от этой точки до отвечающей этому фокусу директрисьг 1), равно эксцентриситету е этого эллипса.
Геометрия поворота / Этюды // Математические этюды
Геометрия поворота / Этюды // Математические этюдыМатематические этюды
К списку
Параллельны ли друг другу передние колёса автомобиля при повороте?
Оказывается, что именно геометрия и механика определяют то, как надо поворачивать колёса автомобиля.
Если продолжение оси колёс направлено в центр поворота, то колесо оставляет чёткий след. Чёткая картинка будет, и если несколько осей направлены в центр поворота.
Однако, если продолжение оси колеса направлено не в центр поворота, то колесо катится с проскальзыванием. След будет стёртым, а самое главное, управляемость
транспорта с таким колесом будет тем хуже, чем выше скорость. Итак, для хорошей управляемости продолжения осей колес должны быть направлены в центр поворота.
Что же это значит для четырёхколёсного автомобиля?
Чёткая картинка будет, и если несколько осей направлены в центр поворота.
Однако, если продолжение оси колеса направлено не в центр поворота, то колесо катится с проскальзыванием. След будет стёртым, а самое главное, управляемость
транспорта с таким колесом будет тем хуже, чем выше скорость. Итак, для хорошей управляемости продолжения осей колес должны быть направлены в центр поворота.
Что же это значит для четырёхколёсного автомобиля?
Научимся для начала проходить простой поворот — дугу окружности.
Так как задние колёса в большинстве машин не поворачиваются, то центр окружности поворота должен лежать на продолжении оси этих колёс. Передние колёса необходимо повернуть так, чтобы продолжение оси каждого колеса смотрело в этот же центр. А значит, для хорошей управляемости передние колёса необходимо поворачивать на разные углы, и они будут непараллельны!
Вы скажете, что повороты не всегда являются дугой какой-либо окружности, и уж тем более машина не останавливается для того, чтобы повернуть колёса. Это, конечно, правда, но оказывается, что при любом повороте в каждый момент времени можно считать, что машина едет по дуге некоторой окружности
(радиус и центр которой зависят от момента времени).
Это, конечно, правда, но оказывается, что при любом повороте в каждый момент времени можно считать, что машина едет по дуге некоторой окружности
(радиус и центр которой зависят от момента времени).
Рассмотрим произвольную дорогу. Чтобы по ней можно было ездить, у неё не должно быть острых углов, т.е. средняя линия будет, как говорят в математике, гладкой кривой.
Зафиксируем синюю точку на средней линии и подумаем, каким более простым геометрическим объектом можно заменить кривую в небольшой окрестности нашей точки.
Возьмём произвольную красную точку недалеко от синей. Две точки на плоскости определяют единственную прямую, которую и проведём. Будем двигать красную
точку по кривой к синей. В момент, когда они совпадут, прямая, ими определяемая, будет касательной прямой. Она даёт линейное приближение кривой дороги
в небольшой окрестности зафиксированной точки. Однако при увеличении видно, что дорога и касательная прямая рядом идут на очень маленьком участке.
Справа и слева от синей точки возьмём по красной. Три точки, не лежащие на одной прямой, определяют единственную окружность, которую и проведём. Будем двигать красные точки к синей. В момент, когда они совпадут, получим окружность, которая называется соприкасающейся. Это приближение уже второго порядка, и на увеличении видно, насколько оно лучше. Заметим, что на монотонном участке (возрастания или убывания кривой) соприкасающаяся окружность всегда пересекает кривую, в отличие от касательной, расположенной на таких участках по одну сторону от кривой.
Так как соприкасающаяся окружность для нашей задачи хорошо приближает дорогу и может быть построена в любой её точке, то движение по изгибам дороги
можно рассматривать в каждый момент времени как движение по дуге некоторой окружности. Мгновенные радиус и центр этой окружности зависят, конечно,
от той точки, в которой находится машина.
Таким образом, при движении в произвольном повороте можно считать, что в каждый момент времени машина движется по небольшой дуге некоторой окружности. И наш первый случай — поворот машины по дуге окружности — основной, который и нужно изучать.
Но как достичь того, чтобы при любом повороте колёс продолжение осей смотрело в мгновенный центр поворота?
Оказывается, и здесь на помощь приходит геометрия, а именно известная со школы равнобокая трапеция — четырёхугольник, у которого две стороны, называемые основаниями, параллельны между собой, а боковые стороны равны друг другу. Если правильно подобрать размеры сторон трапеции, то достигается небоходимое для хорошего управления условие — продолжение осей передних колёс пересекается в точке, лежащей на продолжении оси задних колёс. Эта точка и есть мгновенный центр поворота машины.
Придумал такое управление передними колёсами француз, каретных дел мастер Шарль Жанто (Charles Jeantand). Однако для карет, передвигавшихся с малыми скоростями,
это было не так существенно, как для машин, и изобретение Жанто было забыто. Лишь почти через три четверти века два отца автомобилестроения, два немца,
два инженера — Готтлиб Даймлер (Gottlieb Wilhelm Daimler) и Карл Бенц (Karl Friedrich Michael Benz) — изобретая свои автомобили, возвращаются к трапеции Жанто.
В 1889 году Даймлер получает патент на «способ независимого управления передними колёсами с разновеликими радиусами поворота».
А в 1893 году Бенц получает патент на «устройство управления экипажей с тангенциальными к колёсам окружностями управления».
Решив задачу управления передними поворотными колёсами и другие важные технические вопросы, Карл Бенц строит свой первый знаменитый
четырёхколёсный автомобиль «Виктория».
Однако для карет, передвигавшихся с малыми скоростями,
это было не так существенно, как для машин, и изобретение Жанто было забыто. Лишь почти через три четверти века два отца автомобилестроения, два немца,
два инженера — Готтлиб Даймлер (Gottlieb Wilhelm Daimler) и Карл Бенц (Karl Friedrich Michael Benz) — изобретая свои автомобили, возвращаются к трапеции Жанто.
В 1889 году Даймлер получает патент на «способ независимого управления передними колёсами с разновеликими радиусами поворота».
А в 1893 году Бенц получает патент на «устройство управления экипажей с тангенциальными к колёсам окружностями управления».
Решив задачу управления передними поворотными колёсами и другие важные технические вопросы, Карл Бенц строит свой первый знаменитый
четырёхколёсный автомобиль «Виктория».
С точки зрения строгой математики, трапеция не позволяет достичь необходимого условия — чтобы продолжение осей передних колес при любом повороте пересекалось
в точке, лежащей на продолжении задней оси. При использовании трапеции эта точка будет всегда лежать чуть-чуть в стороне от линии задней оси. Зачем же мы столько
обсуждали трапецию, скажете вы? Расстраиваться рано — просто не надо бездумно переносить математическую строгость в технические вопросы. Чтобы точка
пересечения линий передних осей всегда лежала на линии задней оси, необходимо, чтобы длина меньшего основания трапеции немного менялась.
При общей длине этого основания более метра необходимые изменения длины составляют всего около одного сантиметра, а это меньше чем люфты в соединениях
и разрешённые допуски при изготовлении.
При использовании трапеции эта точка будет всегда лежать чуть-чуть в стороне от линии задней оси. Зачем же мы столько
обсуждали трапецию, скажете вы? Расстраиваться рано — просто не надо бездумно переносить математическую строгость в технические вопросы. Чтобы точка
пересечения линий передних осей всегда лежала на линии задней оси, необходимо, чтобы длина меньшего основания трапеции немного менялась.
При общей длине этого основания более метра необходимые изменения длины составляют всего около одного сантиметра, а это меньше чем люфты в соединениях
и разрешённые допуски при изготовлении.
Со времён изобретения первых автомобилей скорости передвижения сильно возросли. Увеличились и требования к управлению передними колёсами.
Кроме того, трапеция — это плоская геометрическая фигура. И такой способ управления передними колёсами может использоваться только при зависимой
передней подвеске — когда колёса жёстко связаны друг с другом и прямая, соединяющая их центры, всегда параллельна плоскости трапеции. Сейчас такое можно встретить на грузовых автомобилях. На современных легковых автомобилях подвеска колёс независима, т.е. они могут ходить
по высоте друг относительно друга. Для управления в повороте такими колёсами применяются более сложные, уже неплоские шарнирные механизмы,
чаще всего с центральным звеном в виде рулевой рейки. Но их расчёт — это тоже задача математиков и механиков.
А исторически они так по-прежнему и называются — рулевой трапецией.
Сейчас такое можно встретить на грузовых автомобилях. На современных легковых автомобилях подвеска колёс независима, т.е. они могут ходить
по высоте друг относительно друга. Для управления в повороте такими колёсами применяются более сложные, уже неплоские шарнирные механизмы,
чаще всего с центральным звеном в виде рулевой рейки. Но их расчёт — это тоже задача математиков и механиков.
А исторически они так по-прежнему и называются — рулевой трапецией.
При повороте автомобиля возникает ещё один вопрос, связанный с геометрией. Длина окружности радиуса R равна, как вы помните, 2πR. Соответственно,
длина дуги, опирающейся на угол α окружности радиуса R, равна αR. При повороте автомобиля по дуге окружности внешнее переднее колесо едет по дуге
окружности большего радиуса, чем внутреннее переднее. Точно так же и заднее внешнее колесо описывает дугу большего радиуса, чем внутреннее заднее. А раз радиусы различаются, то, значит, пути, проходимые внутренним и внешним колёсами одной оси, должны быть тоже различны.
В противном случае колесо будет проскальзывать, и управляемость автомобиля снизится.
А раз радиусы различаются, то, значит, пути, проходимые внутренним и внешним колёсами одной оси, должны быть тоже различны.
В противном случае колесо будет проскальзывать, и управляемость автомобиля снизится.
В случае, когда ось неведущая, т.е. её колёса не толкают автомобиль вперёд, всё просто: каждое колесо вертится со своей скоростью, необходимой для прохождения нужного пути без проскальзывания.
А как же сделать так, чтобы колёса ведущей оси, в нашем случае задней, с одной стороны, постоянно толкали автомобиль вперёд, а с другой стороны, могли вращаться с разными скоростями?
Помогает в этом дифференциал — представитель планетарных механизмов. Планетарным называется механизм, у которого есть сателлиты — шестерни, крутящиеся вокруг подвижных осей.
Вал от мотора, пройдя через коробку передач, отдаёт вращение на «бочку». Бочка же через сателлиты передаёт вращение на левую и правую полуоси ведущей оси. Как бы ни вращались колёса, скорость бочки всегда в два раза медленнее вращения вала, а сумма скоростей полуосей равна удвоенной скорости вала.
Как бы ни вращались колёса, скорость бочки всегда в два раза медленнее вращения вала, а сумма скоростей полуосей равна удвоенной скорости вала.
Если машина едет по прямой и под обоими ведущими колёсами одинаковое покрытие — с одинаковым коэффициентом трения, то колёса забирают от бочки одинаковое количество вращения, и полуоси вращаются (колёса и их полуоси) с одинаковой скоростью.
Но если коэффициенты трения различаются, например, одна сторона машины выезжает с асфальта на грунтовую обочину или попадает на лёд, то… Как же будут себя вести колёса при прохождении этого участка? У колёс неведущей оси всё просто: они независимы друг от друга, им не надо толкать машину, и когда одно из них выкатывается на лёд, то перестаёт крутиться, так как трение с дорогой очень маленькое.
Вот и под левое колесо ведущей оси попадает лёд. Справа трение с асфальтом большое, а слева — со льдом — почти отсутствует. Соответственно, левому
колесу вращаться гораздо проще, и оно начинает забирать на себя всё вращение, отдаваемое бочкой на обе полуоси. При этом сумма скоростей полуосей,
как было отмечено выше, всегда постоянна, но одна полуось не крутится, а вторая — вращается очень быстро. Начать движение из такого положения, когда
одно колесо ведущей оси потеряло связь с дорогой (например, находится на льду), а другое нет — невозможно.
Соответственно, левому
колесу вращаться гораздо проще, и оно начинает забирать на себя всё вращение, отдаваемое бочкой на обе полуоси. При этом сумма скоростей полуосей,
как было отмечено выше, всегда постоянна, но одна полуось не крутится, а вторая — вращается очень быстро. Начать движение из такого положения, когда
одно колесо ведущей оси потеряло связь с дорогой (например, находится на льду), а другое нет — невозможно.
Казалось бы, одни неудобства от этого дифференциала, зачем он тогда нужен? Как раз для решения задачи одновременного толкания ведущей осью машины вперёд и прохождения в поворотах ведущими колесами путей разной длины. Каждое колесо берёт от дифференциала количество движения пропорционально длине его пути, а в сумме всю энергию вала они затрачивают на движение машины вперёд.
Инженеры постоянно пытаются улучшить дифференциал, сохранив его основное свойство, пытаются уменьшить неприятные эффекты — каким-либо способом не давать
крутиться полуосям со слишком большой разницей скоростей. Но по сути, всё и сегодня остаётся таким же, ибо законы геометрии никто не отменял.
Но по сути, всё и сегодня остаётся таким же, ибо законы геометрии никто не отменял.
Смотри также
Поворот передних колёс автомобиля // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 54—55, 306.
Млодзеевский Б. К. К теории управления в автомобилях // Вестник инженеров. 1917. 15 января. Т. 3, № 2. С. 37—41.
Другие этюды раздела «Математика и техника»
Колёсная пара Уголковый отражатель Глубина заложенияМатематические этюды
Проверка геометрии кузова: что такое, как проверить, признаки нарушения геометрии
Проверка геометрии кузова поможет узнать, был ли автомобиль в серьезных авариях. Не помешает она и машине, прошедшей более 100 тысяч километров без ДТП. Рассказываем, как проверить состояние кузова самостоятельно и в сервисном центре.
Что называют геометрией кузова?
Под геометрией автомобиля понимают расположение силовых элементов кузова друг относительно друга. В норме все расстояния соответствуют параметрам, рассчитанным производителем при разработке модели. При появлении отклонений начинаются проблемы.
Чаще всего геометрию кузова проверяют при покупке подержанного автомобиля. Это лучший способ узнать, была ли машина в ДТП. Если осмотр и тесты показывают легкие деформации, вы можете требовать скидку у продавца. При серьезных повреждениях от покупки лучше отказаться.
Мастера-кузовщики также рекомендуют проверять геометрию кузова каждые 100 тысяч километров, даже если машина не была в авариях. Езда по неровным дорогам, сильный износ подвески, наезды на препятствия и даже долгие стоянки с перекосом (например, одной стороной на бордюре) могут деформировать каркас авто. Чем раньше вы займетесь ремонтом, тем меньше проблем будет в будущем.
Какие отклонения обычно выявляет проверка?
- Длина лонжеронов не совпадает — был серьезный удар с одной стороны.

- Смят моторный щит или поперечина позади салона — автомобиль был в тяжелом ДТП, затронувшем почти весь кузов.
- Погнуты стойки крыши — вероятнее всего, машина переворачивалась.
- Дверцы провисают или неплотно закрываются — был боковой удар или у автомобиля очень большой пробег.
- Плохо закрывается капот или багажник — был сильный удар спереди либо сзади.
- Расстояния между колесами отличаются — машину не щадили, кузов деформирован из-за быстрой езды по плохим дорогам.
- Опоры двигателя неровные, мотор перекошен — автомобиль подпрыгивал на неровностях и очень жестко приземлялся.
Как проверить геометрию кузова самостоятельно?
Визуальный осмотр
Начните со стекол. Верный признак нарушения геометрии кузова — горизонтальные трещины. Деформированный кузов сильно сдавливает стекло, поэтому со временем оно начинает лопаться.
Откройте водительскую дверь, покачайте вверх-вниз, закройте. Если она сильно шатается и стучит, петли установлены неровно или ослаблены. Если дверца закрывается с большим усилием, проем наверняка перекошен.
Если она сильно шатается и стучит, петли установлены неровно или ослаблены. Если дверца закрывается с большим усилием, проем наверняка перекошен.
Посмотрите на зазоры между кузовными панелями, приложите к ним палец для оценки размеров. Неровные щели означают, что машина побывала в серьезной аварии. Еще один повод насторожиться — неоднородная окраска. Разница в цвете говорит о том, что автомобиль красили. В большинстве случаев кузовной ремонт делают после ДТП.
Проверка рулеткой
Структура кузова автомобиля может быть сложной, поэтому геометрию лучше всего проверять по колесам. Вначале измерьте колесную базу справа и слева — расстояние между передней и задней ступицей. Цифры должны быть одинаковы. Затем уточните колею спереди и сзади — дистанцию от середины протектора правого колеса до середины протектора левого. Здесь допускаются различия, поэтому результаты лучше сверять с техническими характеристиками автомобиля. Их можно найти в инструкции по эксплуатации или в интернете.
Можно проверить геометрию кузова своими руками, замерив ширину дверного проема автомобиля у нижней и верхней петли. Посмотрите на длину проема багажника от крышки до кромки в 2–3 точках, а также длину подкапотного пространства. Разница в пару миллиметров допустима — мы уже говорили о последствиях езды по некачественным дорогам. А вот более серьезные отклонения будут поводом насторожиться.
h3 Профессиональная проверка геометрии кузова в автосервисе
Проверка инструментами
Специалисты измеряют расстояние между контрольными точками электронным штангенциркулем с погрешностью не более 0,1 мм. Они оценивают взаимное положение кузовных панелей и силовых элементов с разных сторон, сравнивая результаты между собой.
Для измерения колесной базы, колеи и длины лонжеронов используется масштабная рейка. Мастер устанавливает ее рядом с автомобилем и выбирает нужные точки замера — на экране появляется точное расстояние.
Автоматизированная проверка
Крупные СТО и официальные сервисные центры используют компьютерные стенды. Автомобиль загоняют на подъемник, а затем приклеивают метки к контрольным точкам. Камеры измеряют основные показатели геометрии кузова за считанные секунды.
Автомобиль загоняют на подъемник, а затем приклеивают метки к контрольным точкам. Камеры измеряют основные показатели геометрии кузова за считанные секунды.
В официальных сервисных центрах Mercedes-Benz, Porsche, Cadillac и других престижных брендов могут использоваться лазерные стенды. Они проверяют геометрию кузова автомобиля без меток, сравнивая ее с параметрами завода-изготовителя. Автоматика исключает человеческий фактор — погрешность измерения не превышает 0,5 %.
Чем плоха нарушенная геометрия кузова?
Хуже всего, что поврежденный автомобиль непредсказуемо ведет себя в последующих ДТП. Нередки случаи, когда при легких столкновениях блокируются двери, смещается руль и перекашивает двигатель. Системы пассивной безопасности, заложенные производителем на стадии проектирования, перестают работать и наносят дополнительный вред пассажирам.
Есть и другие неприятные последствия нарушенной геометрии:
- ускоренный износ подвески, полуосей и шин;
- посторонние звуки на малой скорости;
- попадание пыли, воды и грязи в салон;
- неплотно закрывающиеся двери, которые легко взломать;
- ошибки электроники;
- сильные вибрации и тряска на малейших неровностях;
- увод автомобиля в сторону на скорости 50–100 км/ч.

Как исправить геометрию автомобиля?
Ремонтом занимаются специализированные кузовные СТО. Машину разбирают, чтобы добраться до силовой структуры. Мастер проводит замеры по контрольным точкам, чтобы определить степень деформации с точностью до миллиметра.
Геометрию кузова автомобиля восстанавливают на стапелях. Их крюки цепляются за технологические отверстия в каркасе машины. Специалист выбирает расстояние, на которое нужно сместить силовые элементы. Высокоточная гидравлика выполняет его команды, подтягивая крюки цепями.
Нужно помнить, что у металла есть предел прочности. Сильные удары нарушают его структуру на молекулярном уровне, вызывая «усталость». Если кузов серьезно поврежден, проблемы будут появляться даже после восстановления геометрии. Поэтому при покупке подержанной машины нужно знать, в каких авариях она побывала.
24.06.2021
Метод координат — Геометрия — Презентации
\
ось абсцисс
ось аппликат
z
Начало координат —
точка O
Оси координат —
Ox, Oy, Oz
y
ось ординат
О
Координатные плоскости
«Геометрия 7-9» Л. С. Атанасян и др.
С. Атанасян и др.
Oxy, Oyz, Ozx
Система координат
x
Oxyz
2
Положительная полуось
Положительная полуось
Отрицательная полуось
Отрицательная полуось
z
Луч, направление которого совпадает с направлением оси, называется положительной полуосью ,
а другой луч – отрицательной полуосью
О
Отрицательная полуось
Положительная полуось
y
«Геометрия 7-9» Л.С. Атанасян и др.
x
3
В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются координатами точки
z
M 3
M
y
M (x; y; z)
О
M 2
x = OM 1
абсцисса
«Геометрия 7-9» Л.С. Атанасян и др.
M 1
y = OM 2
ордината
z = OM 3
x
аппликата
4
z
I I I I I I I I
I I I I I I I I I I I
O (0; 0; 0)
N (5; 0; 0)
D
F (0; -2; 0)
D (0; 0; 4)
F
M
О
R (0; 0; -0,5)
I I I I I I I I I
y
R
M (0; 3; 0)
«Геометрия 7-9» Л. С. Атанасян и др.
С. Атанасян и др.
S ( x ; 0; 0)
Ox
N
P (0; y ; 0)
Oy
x
T (0; 0; z )
Oz
5
z
I I I I I I I I I I I
I I I I I I I I
N ( 5 ; 4 ; 0)
C (2;-1; 0)
R (-3; -3; 0)
A
F (0; 4; 3)
F
A (0; -3; 4)
R
M (7; 0; 2)
О
y
I I I I I I I I I
D (6; 0;-3)
M
C
«Геометрия 7-9» Л.С. Атанасян и др.
S ( x ; y ; 0)
Oxy
N
Oyz
P (0; y ; z )
x
Oxz
T ( x ; 0; z )
D
6
Точка лежит
На оси
В координатной плоскости
Ox ( x ; 0; 0)
Oxy ( x ; y ; 0)
Oyz (0; y ; z )
Oy (0; y ; 0)
«Геометрия 7-9» Л. С. Атанасян и др.
С. Атанасян и др.
Oxz ( x ; 0; z )
Oz (0; 0; z )
7
z
I I I I I I I I I I I
I I I I I I I I
I I I I I I I
I I I I I I
I I
I I I
I I I I I I I I
I I I I I
A (4;-2,5; 7)
A
S
R
S (5; 4; 8)
N
D (5; 4;-3)
F (-3; 3;-7)
N (0; 0; 4)
О
I I I I I I I I I
y
R (-2;-3; 4)
«Геометрия 7-9» Л.С. Атанасян и др.
M (7; 0;-1)
C
x
I I I
C (7; 4;-1)
M
D
F
8
z
I I I I I I I I
I I I I I I I I
k
j
i
, и – координатные векторы
i
=1;
Координатные векторы не компланарны. Поэтому любой вектор можно разложить по координатным векторам, т. е. представить в виде
е. представить в виде
причем коэффициенты разложения определяются единственным образом.
j
=1;
F
k
разложение вектора по координатным векторам
=1
p
k
p = x i + y j + z k
O
y
I I I I I I I I
i
j
«Геометрия 7-9» Л.С. Атанасян и др.
p{ x; y; z} координаты вектора
F ( x; y; z )
x
9
z
I I I I I I I I
I I I I I I I I
I I I I I I I
Вектор, начало которого совпадает с началом координат – радиус-вектор.
S
p
Координаты радиус-вектора совпадают с координатами конца вектора.
k
S ( 4; 5 ; 8)
O
I I I I I I I I
y
i
j
p {4; 5 ; 8 }
«Геометрия 7-9» Л. С. Атанасян и др.
С. Атанасян и др.
p =4 i + 5 j + 8 k
x
10
z
I I I I I I I I
I I I I I I I I
I I I
I I I I I
I I
OT {4; 5 ; 0}
R
OD {-1; 3; 3}
D
OF {-1; 3;-6}
OM {5; 0; 0}
k
OE {6; 0; 3}
N
O
y
I I I I I I I I
i
j
ON {0; -3; 0}
E
«Геометрия 7-9» Л.С. Атанасян и др.
OR {-2; -3; 4}
T
M
x
F
11
z
I I I I I I I I
I I I I I I I I
0 {0;0;0}
O ( 0; 0; 0 )
0 =0 i + 0 j + 0 k
i {1;0;0}
j {0;1;0}
e
k
r
O
I I I I I I I I
y
i
j
k {0;0;1}
f
«Геометрия 7-9» Л. С. Атанасян и др.
С. Атанасян и др.
e = – i
e {-1;0;0}
r = – j
r {0;-1;0}
x
f {0;0;-1}
f = – k
12
AB a
AB
A
A
a
B
B
Перпендикуляр на прямую
«Геометрия 7-9» Л.С. Атанасян и др.
Перпендикуляр на плоскость
13
x
Oxz
Найти проекции точки М на координатные плоскости.
Oyz
z
M ( x ; y ; z )
M 2
z
M
M 3
y
y
О
Oxy
M M 1 ( x; y; 0)
«Геометрия 7-9» Л.С. Атанасян и др.
Oyz
M 1
M M 2 ( 0 ; y; z )
Oxy
Oxz
x
M M 3 ( x; 0 ; z )
14
x
Oxz
Найти проекции точки М на оси координат.
Oyz
z
M 3
M ( x ; y ; z )
z
M
y
О
y
M 2
Ox
M M 1 ( x; 0 ; 0)
«Геометрия 7-9» Л.С. Атанасян и др.
M 1
Oy
M M 2 ( 0 ; y; 0 )
Oxy
Oz
x
M M 3 (0 ; 0 ; z )
15
z
I I I I I I I I
I I I I I I I I
I I I I I I I
Координаты равных векторов равны.
S
c = p
p
p {4; 5 ; 8 }
c
k
c {4; 5 ; 8 }
O
y
I I I I I I I I
i
j
«Геометрия 7-9» Л.С. Атанасян и др.
x
16
z
I I I I I I I I I I
I I I I I I I I
I I I
I I
1) Какой из данных векторов равен вектору
E
3 i – 2 k
О M =
R
2 ) Напишите разложение
вектора ОЕ
по координатным векторам
, и
D
= -2 i + 3 k
k
k
i
j
y
N
O
I I I I I I
3 ) Найдите координаты
вектора О R
j
i
{- 2 ;-3; 3}
T
4 ) Какой вектор имеет
координаты
{2;3;0}
О T
5 ) Отложите от т. О вектор с координатами
О вектор с координатами
x
M
{- 2 ; 3; 2}
О D
17
№ 405
АСВОА 1 С 1 В 1 О 1 прямоугольный параллелепипед.
Найти координаты векторов
z
{ 2 ; 0 ; 2 }
{ 2 ; 0 ; 2 }
O А 1
B 1
O 1
{ 0 ; 3 ; 2 }
{ 0 ; 3 ; 2 }
O В 1
C 1
2
{ 0 ; 0 ; 2 }
O О 1
A 1
y
3
О
{ 2 ; 3 ; 0}
O С
B
2
{ 2 ; 3 ; 2 }
O С 1
A
«Геометрия 7-9» Л.С. Атанасян и др.
C
ВС 1
АС 1
x
{ 2 ; 3 ; -2 }
О 1 С
18
Координаты вектора
Разложение вектора по координатным векторам
a {-6; 9; 5}
a = – 6 i + 9 j + 5 k
?
n = – 8 i + k
?
n {-8; 0; 1}
c {0; -7; 0}
?
c = – 7 j
m {4; 0; 0}
?
m =4 i
r {-5;-8; 3}
r = –5 i – 8 j +3 k
?
«Геометрия 7-9» Л. С. Атанасян и др.
С. Атанасян и др.
s {-7; 1; 0}
?
s = –7 i + j
e {0;3; 21}
?
e = 3 j + 21 k
q {0; 0; 2}
q =2 k
?
19
Координаты вектора
Разложение вектора по координатным векторам
a {-6; 9; 5}
a = – 6 i + 9 j + 5 k
n = – 8 i + k
n {-8; 0; 1}
c {0; -7; 0}
c = – 7 j
m {4; 0; 0}
m =4 i
r {-5;-8; 3}
r = –5 i – 8 j +3 k
«Геометрия 7-9» Л.С. Атанасян и др.
s {-7; 1; 0}
s = –7 i + j
e {0;3; 21}
e = 3 j + 21 k
q {0; 0; 2}
q =2 k
20
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
1 0
Рассмотрим векторы
a { x 1 ; y 1 ; z 1 }
x 1 i +y 1 j +z 1 k
a = x 1 i +y 1 j +z 1 k
b { x 2 ; y 2 ; z 2 }
x 2 i +y 2 j +z 2 k
b = x 2 i +y 2 j +z 2 k
a+b = + =
«Геометрия 7-9» Л.С. Атанасян и др.
= ( x 1 + x 2 ) i + (y 1 + y 2 ) j + (z 1 + z 2 ) k
a +b { x 1 +x 2 ; y 1 +y 2 ; z 1 +z 2 }
21
b {0; 7;-1} ,
a {3; -5; 2} ,
Даны векторы
№ 407
2
c { ; 0; 0} ,
d {-2,7; 3,1; 0,5}
3
Найдите
2
c { ;0; 0}
2
{ ;7;-1}
a {3;-5;2}
c +b
+
3
+
3
a {3;-5; 2}
b {0;7;-1}
{-2,7; 10,1; -0,5}
d +b
2
c +a { 3 ;-5;2}
a +b {3;2;1}
{0,3; -1,9; 2,5}
a +d
3
«Геометрия 7-9» Л. С. Атанасян и др.
С. Атанасян и др.
2
{3 ; 2; 1}
a +b +c
3
{0,3; 5,1; 1,5}
a +b +d
22
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
2 0
Рассмотрим векторы
a { x 1 ; y 1 ; z 1 }
x 1 i +y 1 j +z 1 k
a = x 1 i +y 1 j +z 1 k
b { x 2 ; y 2 ; z 2 }
b = x 2 i +y 2 j +z 2 k
x 2 i +y 2 j +z 2 k
a –b = – =
( )
«Геометрия 7-9» Л.С. Атанасян и др.
= ( x 1 – x 2 ) i + (y 1 – y 2 ) j + (z 1 –z 2 ) k
a –b { x 1 –x 2 ; y 1 –y 2 ; z 1 – z 2 }
23
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
3 0
a { x ; y ; z }
a {-2; 1;0}
3
Рассмотрим вектор
3 a {-6; 3; 0}
a = x i +y j +z k
k
a {-2; 0; 3}
(-2)
ka = kx i +ky j +kz k
-2 a {4; 0;-6}
«Геометрия 7-9» Л.С. Атанасян и др.
ka { kx ; ky ; kz }
a {-2; 5 ;-3}
(- 1 )
— a { 2; -5 ; 3}
24
a — b
Найдите координаты вектора
a {-6; 9;1}
a {-6; 9;1}
a {-6; 9;1}
b {-8;12;-3}
b {-8;12;-3}
b {-8;12;-3}
2 способ
1 способ
(-1)
—
+
a — b {2;-3; 4}
«Геометрия 7-9» Л.С. Атанасян и др.
-b {8;-12;3}
a — b {2;-3; 4}
25
a — b
№ 409
Найдите координаты вектора , если
1) a {5;-1; 1}; b {-2;1; 0}
1 способ
2 способ
b {-2;1; 0}
(-1)
a {5;-1; 1}
—
b {-2;1; 0}
a {5;-1; 1}
«Геометрия 7-9» Л. С. Атанасян и др.
С. Атанасян и др.
+
a — b {7;-2; 1}
-b {2;-1; 0}
a — b {7;-2; 1}
26
№ 4 10
Даны векторы
c {2; 1;-3}
c {2; 1;-3}
a {-1; 2; 0}
b {0;-5;-2}
b {0;-5;-2}
a {-1; 2; 0}
p
p = 3 b – 2 a + c
Найдите координаты вектора
3
3)
1)
3 b {0;-15;-6}
3 b {0;-15;-6}
+
(-2)
2)
-2 a {2;-4; 0}
-2 a {2;-4; 0}
{4;-18;-9}
3 b – 2 a + c
27
Найдите координаты остальных вершин куба.
z
D 1
C 1
A 1
B 1
D
C
y
О
«Геометрия 7-9» Л.С. Атанасян и др.
A
B( 3 ; 3 ;0)
x
28
Найдите координаты остальных вершин куба.
z
D 1
C 1
A 1
B 1
D
C
y
О
A
«Геометрия 7-9» Л.С. Атанасян и др.
B( 4 ; 8 ;0)
x
29
№ 4 08
Найдите координаты векторов
OP.
OM,
AC,
BM,
CB,
AB,
MN,
NP,
OA=4
z
OB=9
M, N P – середины отрезков АС, ОС и ВС
OC=2
С
Р
N
y
k
j
М
В
O
i
А
= –4 i + 2 k
= A О + ОС
Из АОС ,
= –О A + ОС
AC
x
AC {-4; 0 ; 2}
30
THE RESEARCH ON THE FAMILIES CONFOCAL ELLIPSES AND HYPERBOLAS THROUGH GEOGEBRA MATHEMATICAL PACKAGE
ИССЛЕДОВАНИЕ СЕМЕЙСТВ СОФОКУСНЫХ ЭЛЛИПСОВ И ГИПЕРБОЛ СРЕДСТВАМИ МАТЕМАТИЧЕСКОГО ПАКЕТА GEOGEBRA
Научная статья
Пронина Е. В.*
В.*
Российский технологический университет, Москва, Россия
* Корреспондирующий автор (elenavladpronina[at]rambler.ru)
Аннотация
В статье приведено задание семейств софокусных эллипсов и гипербол и исследование их свойств средствами математического пакета GeoGebra в курсе «Аналитической геометрии» при изучении темы «Кривые второго порядка» студентами технического вуза. Основной целью статьи является демонстрация интеграции современных информационных технологий в процесс преподавания высшей математики. С помощью встроенных инструментов и команд среды GeoGebra поэтапно показано задание и построение софокусных эллипсов и гипербол. С использованием динамических чертежей рассмотрен процесс «трансформации» одной коники в другую при различных значениях задаваемых параметров. Опираясь на свойства касательных к кривым второго порядка, установлено и исследовано, что софокусные эллипс и гипербола пересекаются под прямым углом. Последний результат рассмотрен для различных случаев взаимного расположения кривых и касательных к ним, проведённых в точке их пересечения. Все полученные результаты обоснованы строго математически.
Последний результат рассмотрен для различных случаев взаимного расположения кривых и касательных к ним, проведённых в точке их пересечения. Все полученные результаты обоснованы строго математически.
Ключевые слова: GeoGebra, преподавание математики, кривые второго порядка, эллипс, гипербола, касательные к коникам, оптические свойства коник, софокусные коники, углы между кривыми.
THE RESEARCH ON THE FAMILIES CONFOCAL ELLIPSES AND HYPERBOLAS THROUGH GEOGEBRA MATHEMATICAL PACKAGE
Research article
Pronina E.V.*
Russian Technological University, Moscow, Russia
* Corresponding author (elenavladpronina[at]rambler.ru)
Abstract
The article describes setting the families of confocal ellipses and hyperbolas and studying their properties through the GeoGebra mathematical package in the course «Analytic geometry» under the topic «Second-order curve» by the students of a technical college. The primary purpose of the article is to demonstrate the integration of modern information technology into the process of teaching higher mathematics. Using the built-in tools and commands of the GeoGebra environment, the setting and construction of confocal ellipses and hyperbolas are shown step-by-step. Using the dynamic drawings, the author considers the process of «transformation» of one conic into another at different values of the specified parameters. Relying on the properties of a tangent to a second-order curve, the author found and analyzed that the confocal ellipse and the hyperbola intersect at a right angle. The last result is considered for various cases of the mutual arrangement of curves and tangents at the point of their intersection. All the results obtained are justified strictly mathematically.
The primary purpose of the article is to demonstrate the integration of modern information technology into the process of teaching higher mathematics. Using the built-in tools and commands of the GeoGebra environment, the setting and construction of confocal ellipses and hyperbolas are shown step-by-step. Using the dynamic drawings, the author considers the process of «transformation» of one conic into another at different values of the specified parameters. Relying on the properties of a tangent to a second-order curve, the author found and analyzed that the confocal ellipse and the hyperbola intersect at a right angle. The last result is considered for various cases of the mutual arrangement of curves and tangents at the point of their intersection. All the results obtained are justified strictly mathematically.
Keywords: GeoGebra, teaching mathematics, second-order curves, ellipse, hyperbola, tangents to conics, optical properties of conics, confocal conics, angles between curves.
Введение
В курсе «Аналитическая геометрия» в техническом вузе предусмотрено изучение темы «Кривые второго порядка». Для решения сложных задач, выходящих за рамки программы, к сожалению, не всегда остаётся время. Одним из таких вопросов является вопрос рассмотрения софокусных коник и их свойств. Его рассмотрение удобно организовать с помощью динамических чертежей математического пакета GeoGebra, позволяющего моделировать и решать различные геометрические задачи, проводить анализ геометрической конфигурации объектов, строить графики функций, получать изображения плоских фигур и устанавливать связи между их элементами, проводить дополнительные построения, создавать анимацию рисунков.
Динамичность используемой математической среды полностью отвечает современным запросам общества для быстрого, правильного и наглядного получения результата, проверки гипотез. В результате подобной интеграции современных информационных технологий в образовательный процесс вуза происходит приобщение студентов к исследовательской деятельности средствами научных разработок в области информатики, что позволяет повысить мотивацию обучения и общую компьютерную грамотность обучающихся.
Процесс моделирования задачи, её пошаговое результативно-визуальное решение с помощью динамических чертежей способствует систематизации, глубокому пониманию и усвоению теоретических основ темы, а также, формированию навыков, связанных с применением математических методов в конструировании объектов.
Исследование общих свойств софокусных коник средствами пакета GeoGebra
В этом разделе рассмотрим общее задание софокусных коник и изучим процесс трансформации одной коники в другую средствами пакета GeoGebra. Поскольку основной целью статьи является демонстрация интеграции пакета GeoGebra в учебный процесс, будем приводить обоснования получаемых результатов.
Зададим на плоскости две точки . Не нарушая общности, будем полагать, что они находятся на оси абсцисс. Рассмотрим семейство всех эллипсов и гипербол, для которых являются фокусами. Такие эллипсы и гиперболы называются софокусными. Центры эллипса и гиперболы совпадают и находятся в начале координат.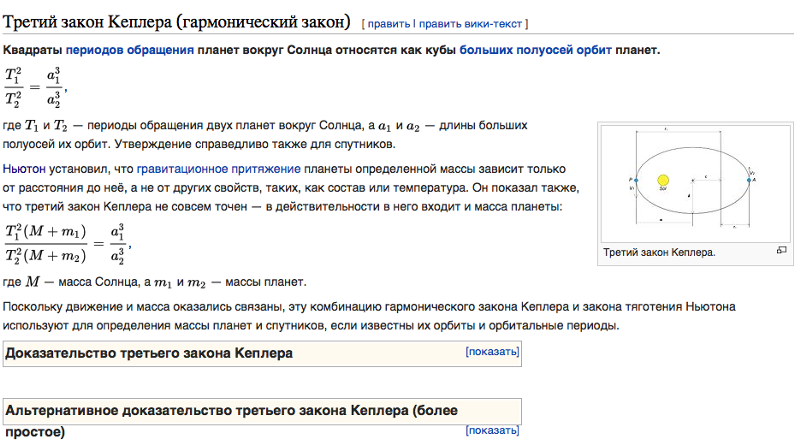 Большая ось эллипса и действительная ось гиперболы находятся на оси Ox, малая ось эллипса и мнимая ось гиперболы находятся на оси Oy.
Большая ось эллипса и действительная ось гиперболы находятся на оси Ox, малая ось эллипса и мнимая ось гиперболы находятся на оси Oy.
Уравнение произвольной линии рассматриваемого семейства можно записать в виде – каноническое уравнение семейства софокусных эллипсов и гипербол. При этом параметр .
Реализация в среде GeoGebra
Шаг 1. Зададим значение параметра c (для примера произвольно, например, c=4)
В строке ввода введём с=4.
Для дальнейших исследований можно задать диапазон значений параметра c. Для этого необходимо выбрать появившийся «бегунок» и установить границы изменения параметра, например, от 0 до 4.
Шаг 2. Зададим фокусы
В строке ввода введём F1=(-c,0).
В строке ввода введём F2=(c,0).
Шаг 3. Зададим значение параметра a (для примера произвольно, соблюдая )
В строке ввода введём a=6.
Шаг 4. Зададим значение параметра b
Зададим значение параметра b
В строке ввода введём
Шаг 5. Зададим значение параметра t. В качестве начального значения выберем t=0.
В строке ввода введём
Шаг 6. Теперь непосредственно зададим конику.
В строке ввода введём
Результат выполнения шагов 1-6 представлен на рисунке 1.
Рис. 1 – Результат выполнения шагов 1-6
Рассмотрим возможные значения параметра t.
- . В этом случае . Очевидно, нет точек плоскости, координаты которых удовлетворяли бы уравнению кривой.
Рассмотрим случай 1 в среде GeoGebra.
Шаг 7. Для параметра t введём границы изменения, например, от -50 до с шагом 1, см. рисунок 2.
Рис. 2 – Результат выполнения шага 7
Нажав на кнопку , запустим бегунок и убедимся, что нет точек плоскости, координаты которых удовлетворяли бы заданному параметру. Обратите внимание, при для g появляется значение «не определено».
Обратите внимание, при для g появляется значение «не определено».
- . В этом случае множеством точек плоскости, удовлетворяющим заданию кривой g, является гипербола. С действительной полуосью и мнимой полуосью .
Рассмотрим случай 2 в среде GeoGebra.
Шаг 8. Для параметра t введём границы изменения от с шагом 1.
Нажав на кнопку , запустим бегунок и убедимся, что при каждом значении параметра t получается гипербола. Можно заметить, что при слева, гипербола сжимается к оси Ox, что соответствует уменьшению мнимой полуоси гиперболы. При справа, гипербола сжимается к оси Oy, что соответствует уменьшению действительной полуоси гиперболы.
- . В этом случае множеством точек плоскости, удовлетворяющим заданию кривой g, является эллипс. С большой полуосью и малой полуосью .
Рассмотрим случай 3 в среде GeoGebra.
Шаг 9. Для параметра t введём границы изменения от до, например, 50 с шагом 1.
Для параметра t введём границы изменения от до, например, 50 с шагом 1.
Нажав на кнопку , запустим бегунок и убедимся, что при каждом значении параметра t получается эллипс. Можно заметить, что при справа, большая полуось эллипса стремится к c, тогда как малая стремится к нулю и эллипс сжимается к оси Ox. При эллипс «округляется», поскольку его эксцентриситет стремится к единице.
Если теперь для параметра t задать границы изменения, например, от -50 до 50 с шагом 1, то можно с помощью динамического чертежа проследить весь процесс трансформации, описанный в случаях 1-3 и реализованный в шагах 7-8.
Приложение свойств касательных к семействам софокусных коник
В этом разделе, используя пакет GeoGebra, исследуем экспериментально один очень интересный результат, относящийся к семейству софокусных коник и часто остающийся за пределами вузовской программы.
- Постановка задачи
Доказать, что любые эллипс и гипербола из семейства софокусных коник пересекаются под прямым углом.
Углом между двумя пересекающимися кривыми называется угол между касательными к ним в точке их пересечения.
Будем считать, что фокусы коник расположены на оси Ox. В этом исследовании предусмотрим случай, когда центр эллипса и гиперболы может быть смещён относительно начала координат, при этом оси симметрии эллипса и гиперболы остаются параллельны осям Ox и Oy.
На первом шаге зададим фокусы, затем вычислим половину фокусного расстояния c. Для обобщения результатов исследования, длину большой полуоси эллипса и главной оси гиперболы будем задавать в некоторых границах больше или меньше параметра c соответственно.
Далее рассмотрим решение задачи только в среде GeoGebra.
- Реализация в среде GeoGebra
Шаг 1. Зададим фокусы эллипса и гиперболы.
В строке ввода введём F1=(-4,0) и F2=(4,0) (например).
Шаг 2. Вычислим половину фокусного расстояния c.
В строке ввода введём с=(abs(x(F1))+ abs(x(F2)))/2.
Шаг 3. Зададим большую полуось эллипса, назвав её аэ.
В строке ввода введём аэ=5 (например).
Далее, нажав на появившийся бегунок, зададим границы изменения большой полуоси от c+1 до 10 (например), шаг 1.
Шаг 4. Зададим действительную полуось гиперболы, назвав её аг.
В строке ввода введём аг=3 (например).
Далее, нажав на появившийся бегунок, зададим границы изменения действительной полуоси от 1 до с-1 (например), шаг 1.
Шаг 5. Построим эллипс.
В строке ввода введём Эллипс(F1,F2,аэ).
Изменим цвет, например, на синий. Для этого необходимо щёлкнуть правой кнопкой мыши на кривой, далее выбрать Настройки→Цвет.
Шаг 6. Построим гиперболу.
В строке ввода введём Гипербола(F1,F2,аг).
Изменим цвет, например, на зелёный.
Шаг 7. С помощью инструмента «Точка»→«Пересечение», найдём точки пересечения эллипса и гиперболы.
Результат выполнения шагов 1-7 представлен на рисунке 3.
Рис. 3 – Результат выполнения шагов 1-7
Перейдём к построению касательных к кривым и нахождению угла между ними.
Шаг 8. С помощью инструмента «Касательная», построим касательную к эллипсу в одной из точек пересечения эллипса и гиперболы. Например, в точке B.
Шаг 9. С помощью инструмента «Касательная», построим касательную к гиперболе также в точке B.
Шаг 10. С помощью инструмента «Угол», найдём угол между построенными касательными.
Результат выполнения шагов 1-10 представлен на рисунке 4.
Рис. 4 – Результат выполнения шагов 1-10
Шаг 11. С помощью инструмента «Бегунок» будем менять значения параметров аэ и аг. Формы эллипса и гиперболы будут изменяться, но угол между ними будет оставаться прямым. Один из примеров приведён на рисунке 5.
Рис.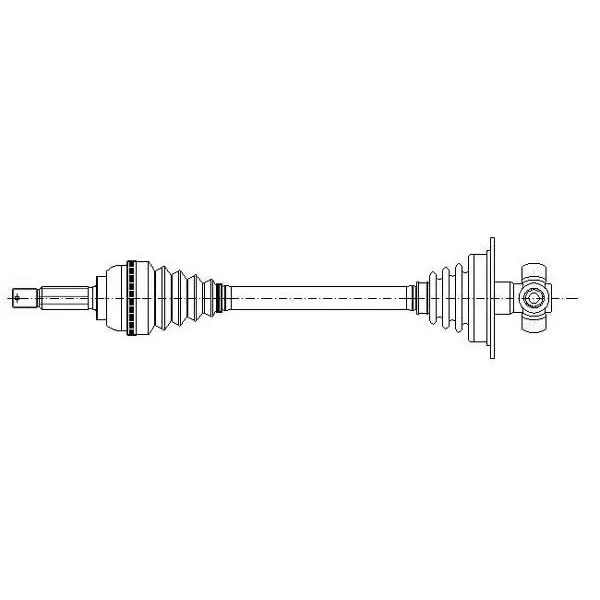 5 – Пример изменения значения параметров аэ и аг
5 – Пример изменения значения параметров аэ и аг
Шаг 12. Поменяем фокусы, сместив центры кривых. Как видно из рисунка, угол между эллипсом и гиперболой также останется прямым.
Рис. 6 – Угол между эллипсом и гиперболой
Поскольку параметры были выбраны произвольно, то полученный динамически результат доказывает, что любые эллипс и гипербола из семейства софокусных коник пересекаются под прямым углом.
Выводы
Использование динамических чертежей математического пакета GeoGebra позволяет значительно упростить рассмотрение сложных задач аналитической геометрии, требующих большой визуализации, а также расширить спектр рассматриваемых задач. Кроме того, наглядность полученного с помощью пакета GeoGebra результата способствует глубокому усвоению и пониманию геометрических основ физических явлений. А, следовательно, и более простому их дальнейшему использованию в инженерных расчётах.
А, следовательно, и более простому их дальнейшему использованию в инженерных расчётах.
Данный материал может быть использован на семинарских и факультативных занятиях со студентами, для организации самостоятельной научно-исследовательской деятельности учащихся или дистанционного обучения.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Акопян А.В. Геометрические свойства кривых второго порядка / А.В. Акопян, А.А. Заславский. – М.:МЦНМО, 2007. -136с.
- Безумова О.Л. Обучение геометрии с использованием возможностей GeoGebra/ Безумова О.Л., Овчинникова Р.П. и др. Архангельск, Изд. ООО «Кира», 2011. – 140 с.
- Есаян А.Р. Преобразования объектов в GeoGebra / А.Р. Есаян, Н.М. Добровольский // Чебышевский сб., 2017. Т.18, вып.2. С.129-143.
- Есаян А.
 Р. Динамическая образовательная среда GeoGebra / А.Р. Есаян, Н.М. Добровольский, Е.А. Седова, А.В. Якушин– Тула: Извд-во Тул.гос.пед.ун-та им. Л.Н.Толстого, 2017. – Ч.1. – 417 с.
Р. Динамическая образовательная среда GeoGebra / А.Р. Есаян, Н.М. Добровольский, Е.А. Седова, А.В. Якушин– Тула: Извд-во Тул.гос.пед.ун-та им. Л.Н.Толстого, 2017. – Ч.1. – 417 с. - Есаян А.Р. Экспериментальное обоснование гипотез в GeoGebra / А.Р. Есаян, А.В. Якушин // Чебышевский сб., 2017. Т.18, вып.1. С.92-108.
- Заславский А.А. Геометрические преобразования / А.А. Заславский. М.: МЦМНО, 2004. – 86 с.
- Краснов М.Л. Вся высшая математика: Учебник. Т. 1. Изд.4-е / М.Л. Краснов, А.И. Киселев, Г.И Макаренко и др. – М. Едиториал УРСС, 2012. – 336 с.
- Ларин С.В. Методика обучения математике: Компьютерная анимация в среде GeoGebra: учебное пособие для вузов / С.В. Ларин. – М.Издательство Юрайт, 2018. – 233 с.
- Лубягина Е.Н. Опыт организации учебно-исследовательской деятельности студентов при изучении кривых второго порядка / Е.Н. Лубягина, Л.В. Тимшина // Вестник Сыктывкарсого университета. Серия 1: Математика. Механика.
 Информатика. – 2017. – № 2 (23). – С. 71-84.
Информатика. – 2017. – № 2 (23). – С. 71-84. - Постников М.М. Аналитическая геометрия / М.М. Постников. – М.: «Наука», 1973. – 754с.
- Смирнов В.А. Геометрия с GeoGebra. Планиметрия / В.А. Смирнов, И.М. Смирнова. – М.: «Прометей», 2018. – 206с.
- Смирнов В.А. Геометрия с GeoGebra. Стереометрия / В.А. Смирнов, И.М. Смирнова. – М.: «Прометей», 2018. – 172с.
- Чеботарева Э.В. Компьютерный эксперимент с GeoGebra / Э.В. Чеботарева. – Казань: Казанский ун-т, 2015. – 61 с.
- GeoGebra Manual. The official manual of GeoGebra. PDF generated. – 325p.
Список литературы на английском языке / References in English
- Akopyan A.V. Geometricheskie svojstva krivy`x vtorogo poryadka [Geometric properties of second-order curves] / A.V. Akopyan, A.A. Zaslavskii. – M.:MCNMO, 2007. -136p. [in Russian]
- Bezumova O.
 L. Obuchenie geometrii s ispol`zovaniem vozmozhnostej GeoGebra [Teaching geometry using GeoGebra] / Bezumova O.L., Ovchinnikova R.P. et al. Arxangel`sk, Publishing house OOO «Kira», 2011. – 140 p. [in Russian]
L. Obuchenie geometrii s ispol`zovaniem vozmozhnostej GeoGebra [Teaching geometry using GeoGebra] / Bezumova O.L., Ovchinnikova R.P. et al. Arxangel`sk, Publishing house OOO «Kira», 2011. – 140 p. [in Russian] - Yesayan A.R. Preobrazovaniya ob«ektov v GeoGebra / A.R. Yesayan, N.M. Dobrovolskii [Object transformations in GeoGebra] // Cheby`shevskij sb., 2017. V.18, vyp.2. p.129-143. [in Russian]
- Yesayan A.R. Dinamicheskaya obrazovatel`naya sreda GeoGebra [GeoGebra, the dynamic educational environment] / A.R. Yesayan, N.M. Dobrovolskii, E.A. Sedova, A.V. Yakushin. – Tula: Izvd-vo Tul.gos.ped.un-ta im. L.N.Tolstogo, 2017. – Issue1. – 417 p. [in Russian]
- Yesayan A.R. E`ksperimental`noe obosnovanie gipotez v GeoGebra [Experimental justification of hypotheses in GeoGebra] / A.R. Yesayan, A.V. Yakushin. // Cheby`shevskij sb., 2017. V.18, vyp.1. p.92-108. [in Russian]
- Zaslavskii A.A. Geometricheskie preobrazovaniya [Geometric transformations] / A.
 A. Zaslavskii. – M.: MCzMNO, 2004. – 86 p. [in Russian]
A. Zaslavskii. – M.: MCzMNO, 2004. – 86 p. [in Russian] - Krasnov M.L. Vsya vy`sshaya matematika: Uchebnik. V. 1. Ed.4 [All the further mathematics: Textbook. Vol. 1. Ed. 4th] / M.L. Krasnov, A.I. Kiselev, G.I Makarenko, E.V Shikin, V.I. Zalyapin, S.K. Sobolev. – M. Editorial URSS, 2012. – 336 p. [in Russian]
- Larin S.V. Metodika obucheniya matematike: Komp`yuternaya animaciya v srede GeoGebra: uchebnoe posobie dlya vuzov [Mathematics teaching method: Computer animation in the GeoGebra environment: a textbook for universities] / S.V Larin. . – M. Publishing house Yurajt, 2018. – 233 p. [in Russian]
- Lubyagina E.N. Opy`t organizacii uchebno-issledovatel`skoj deyatel`nosti studentov pri izuchenii krivy`x vtorogo poryadka [Experience in organizing educational and research activities of students in the study of second-order curves] / E.N. Lubyagina, L.V. Timshina // Vestnik Sy`kty`vkarsogo universiteta. Seriya 1: Matematika. Mexanika. Informatika.
 – 2017. — № 2 (23). – p. 71-84. [in Russian]
– 2017. — № 2 (23). – p. 71-84. [in Russian] - Postnikov M.M. Analiticheskaya geometriya [Analytical geometry] / M.M. Postnikov. – M.: «Nauka», 1973. – 754p. [in Russian]
- Smirnov V.A. Geometriya s GeoGebra. Planimetriya [Geometry with GeoGebra. Planimetry] / V.A. Smirnov, I.M. Smirnova. – M.: «Prometej», 2018. – 206 p. [in Russian]
- Smirnov V.A. Geometriya s GeoGebra. Stereometriya [Geometry with GeoGebra. Stereometry] / V.A. Smirnov, I.M. Smirnova. – M.: «Prometej», 2018. – 172 p. [in Russian]
- Chebotareva E.V. Komp`yuterny`j e`ksperiment s GeoGebra [Computer experiment with GeoGebra] / E`.V. Chebotareva. – Kazan`: Kazanskij un-t, 2015. – 61 p. [in Russian]
- GeoGebra Manual. The official manual of GeoGebra. PDF generated. – 325p.
Большая полуось — Academic Kids
From Academic Kids
В геометрии большая полуось (также большая полуось ) a применяется к эллипсам и гиперболам.
| Содержимое |
1 Эллипс 2 Гипербола 3 Астрономия 3.1 Период обращения 4 Пример 5 Каталожные номера |
Эллипс
Большая полуось эллипса — это половина большой оси, проходящей от центра через фокус к краю эллипса. Большая ось — это самая длинная линия, проходящая через центр и оба фокуса эллипса, причем ее концы находятся в самых широких точках формы.
Он связан с малой полуосью
и кинетическая энергия равна
Приравнивая энергию Земли в афелии и перигелии, мы получаем
и немного вычислив алгебру:
и найдя
Но помните, что большая и малая полуоси орбиты Земли равны11
011
соответственно! Итак, у нас есть
Это позволяет нам переписать нашу старую формулу для энергии в виде солнечного света, падающего на Землю каждый год:
Но мы также видели, что
, поэтому мы получаем формулу мы искали:
Это говорит нам о функции большой полуоси и эксцентриситета.
Как мы увидим позже, большая полуось практически не изменяется при небольших возмущениях орбиты Земли. Главное, что меняется, это эксцентриситет. Но если мало, то еще меньше, поэтому не сильно меняется, когда мы меняем
Но если мало, то еще меньше, поэтому не сильно меняется, когда мы меняем
Мы можем сделать это более количественным. Давайте выясним, насколько фактические изменения орбиты Земли влияют на количество получаемой ею солнечной радиации! Как мы увидим, большая полуось почти постоянна, так что мы можем игнорировать это. Сложные расчеты, которые мы не можем повторить здесь, показывают, что эксцентриситет варьируется от 0,005 до 0,058. Мы видели, что общая энергия, которую Земля получает каждый год от солнечной радиации, пропорциональна
. Когда эксцентриситет имеет наименьшее значение, мы получаем
Когда эксцентриситет достигает максимального значения, мы получаем
Таким образом, солнечная энергия, падающая на Землю каждый год, изменяется в
раз. Другими словами, она изменяется всего на 0,167%.
Это очень мало И влияние на температуру Земли было бы наивно еще меньше!
Наивно мы можем рассматривать Землю как серое тело : идеальный объект, тенденция которого поглощать или излучать излучение одинакова для всех длин волн и температур. Поскольку температура серого тела пропорциональна четвертому корню из мощности, которую оно получает, изменение солнечной энергии на 0,167%, получаемой в год, соответствует процентному изменению температуры примерно на одну четверть. Это изменение температуры на 0,042%. Если мы представим, что начинаем с такой Земли, как наша, со средней температурой примерно 290 кельвин, это изменение всего на 0,12 кельвина!
Поскольку температура серого тела пропорциональна четвертому корню из мощности, которую оно получает, изменение солнечной энергии на 0,167%, получаемой в год, соответствует процентному изменению температуры примерно на одну четверть. Это изменение температуры на 0,042%. Если мы представим, что начинаем с такой Земли, как наша, со средней температурой примерно 290 кельвин, это изменение всего на 0,12 кельвина!
Вывод выглядит так: в наивной модели без каких-либо усиливающих эффектов изменения эксцентриситета земной орбиты вызвали бы изменение температуры всего на 0,12 °C!
Это намного меньше, чем разница примерно в 5 °C, которую мы наблюдаем между ледниковыми и межледниковыми периодами. Итак, если изменения эксцентриситета важны в ледниковых циклах, нам нужно дать некоторое объяснение. Возможные объяснения включают явления, зависящие от сезона, и эффекты обратной связи с климатом, такие как эффект альбедо льда, который мы обсуждали. Вероятно и очень важны!
Адиабатическая инвариантность
Почему большая полуось орбиты Земли практически не изменяется при малых возмущениях? Причина в том, что это «адиабатический инвариант». Это в основном просто причудливый способ сказать, что он остается почти неизменным. Но дело в том, что существует целая теория адиабатических инвариантов… которая якобы объясняет почти постоянство большой полуоси.
Это в основном просто причудливый способ сказать, что он остается почти неизменным. Но дело в том, что существует целая теория адиабатических инвариантов… которая якобы объясняет почти постоянство большой полуоси.
Согласно Википедии:
Эксцентриситет Земли изменяется в основном из-за взаимодействия с гравитационными полями Юпитера и Сатурна. По мере изменения эксцентриситета орбиты большая полуось орбитального эллипса остается неизменной. С точки зрения теории возмущений, используемой в небесной механике для расчета эволюции орбиты, большая полуось является адиабатическим инвариантом. Согласно третьему закону Кеплера период обращения определяется большой полуосью. Из этого следует, что период обращения Земли, длина звездного года, также остается неизменным по мере эволюции орбиты. Поскольку малая полуось уменьшается с увеличением эксцентриситета, сезонные изменения увеличиваются. Но среднее солнечное излучение для планеты изменяется незначительно при малом эксцентриситете из-за второго закона Кеплера.
К сожалению, хотя я немного разбираюсь в общей теории адиабатических инвариантов, я не удосужился убедить себя в том, что большая полуось является чем-то вроде возмущения, которое испытывает Земля.
Вот кое-что попроще: проверка того, что большая полуось земной орбиты определяет период земной орбиты, скажем . Чтобы сделать это, сначала свяжите угловой момент с периодом, интегрируя скорость, с которой орбитальная площадь сметается планетой:
на одной орбите. Поскольку площадь эллипса равна , это дает нам:
С другой стороны, мы видели
Приравнивание этих двух выражений для показывает, что период равен:
Итак, период зависит на большой полуоси, а не на эксцентриситет. И наоборот, мы могли бы решить это уравнение, чтобы увидеть, что большая полуось зависит только от периода, а не от эксцентриситета.
Лечу и как постоянные здесь. Если масса Солнца уменьшится, как это в конечном итоге произойдет, когда оно станет красным гигантом и выпустит много газа, большие полуоси земной орбиты изменятся. Реально увеличится! Это одна из причин, по которой люди до сих пор спорят о том, когда именно Земля будет поглощена Солнцем:
Реально увеличится! Это одна из причин, по которой люди до сих пор спорят о том, когда именно Земля будет поглощена Солнцем:
• Дэвид Аппелл, Солнце в конце концов поглотит Землю — возможно, Scientific American , 8 сентября 2008 г.
-большая ось орбиты Земли изменится, эксцентриситет останется практически неизменным. Почему? Потому что для этого процесса типа именно эксцентриситет является адиабатическим инвариантом!
Действительно, я очень обрадовался, когда начал читать домашнюю задачу в книге Ландау и Лифшица Классическая механика , описывающая адиабатические инварианты гравитационной задачи двух тел. Но я был расстроен, когда они пришли к выводу, что эксцентриситет является адиабатическим инвариантом для постепенных изменений . Они не обсуждали никаких задач, для которых большая полуось была бы адиабатическим инвариантом.
Когда-нибудь я вернусь к этому позже, возможно, с помощью хорошей книги по небесной механике. Если вам интересно узнать о концепции адиабатического инварианта, начните здесь:
Если вам интересно узнать о концепции адиабатического инварианта, начните здесь:
• Адиабатический инвариант, Википедия.
, а затем попробуйте это:
• Марко Робник, Теория адиабатических инвариантов, февраль 2004 г.
И если вы знаете, как показать, что большая полуось Земли является адиабатическим инвариантом, скажите, пожалуйста, как!
Эта запись была опубликована во вторник, 27 ноября 2012 г., в 23:29 и находится в разделе астрономия, климат, математика. Вы можете следить за любыми ответами на эту запись через ленту RSS 2.0. Вы можете оставить отзыв или вернуться со своего сайта.
microstructpy.geometry.Ellipse — MicroStructPy
- класс microstructpy.geometry.Ellipse( **kwargs )[источник]
Базы:
объектДвухмерная геометрия эллипса.
Этот класс содержит двумерный эллипс. Он определяется центральной точкой, осями и ориентация.
Без каких-либо параметров эллипс по умолчанию представляет собой единичный круг.

- Параметры
a ( float ) – (дополнительно) Большая полуось эллипса. По умолчанию 1.
b ( поплавок ) – (дополнительно) Малая полуось эллипса. По умолчанию 1.
центр ( список ) – (опционально) Центр эллипса. По умолчанию (0, 0).
оси ( список ) – (опционально) 2-элементный список полуосей, эквивалент до
[а, б]. По умолчанию [1, 1].размер ( поплавок ) – (дополнительно) Диаметр круга с эквивалентом область. По умолчанию 1.
aspect_ratio ( float ) – (опционально) Отношение оси x к оси y длина. По умолчанию 1.
угол ( поплавок ) – (дополнительно) Угол поворота против часовой стрелки, в градусах, измеренных от оси +x.

angle_deg ( float ) – (опционально) Угол поворота в градусах.
angle_rad ( float ) – (опционально) Угол поворота в радианах.
матрица ( numpy.ndarray ) — (необязательно) Матрица вращения 2×2.
ориентация ( numpy.ndarray ) – (необязательно) Псевдоним для матрицы
- приблизительный ( x1 = нет ) [источник]
Приближенный эллипс с набором окружностей.
Эта функция преобразует эллипс в набор окружностей. Он реализует опубликованный алгоритм Ильина и Бернаки. 1
Пример
>>> импортировать matplotlib.pyplot как plt >>> импортировать microstructpy как MSP >>> импортировать numpy как np >>> эллипс = msp.geometry.Ellipse(a=3, b=1) >>> приблизительно = эллипс.
 приблизительно(0,7)
>>> приблизительно
массив([[ 0. , 0. , 1. ],
[ 0,7 , 0, 0,96889112],
[1,38067777, 0, 0,87276349],
[2,00213905, 0, 0,7063497],
[2,5234414, 0, 0,45169729],
[2,66666667, 0, 0,33333333],
[-0,7 , 0, , 0,96889112],
[-1,38067777, 0. , 0,87276349],
[-2.00213905, 0. , 0.7063497 ],
[-2,5234414, 0, 0,45169729],
[-2,66666667, 0. , 0,33333333]])
>>> ellipse.plot(edgecolor='k', facecolor='none', lw=3)
>>> t = np.linspace(0, 2 * np.pi)
>>> для x, y, r примерно:
... plt.plot(x + r * np.cos(t), y + r * np.sin(t), 'b')
>>> plt.xticks(np.unique(np.concatenate((приблизительно[:, 0], (-3, 3)))))
>>> plt.yticks(np.unique(np.concatenate((приблизительно[:, 1], (-1, 1)))))
>>> plt.axis('в масштабе')
>>> plt.grid(True, linestyle=':')
>>> plt.show()
приблизительно(0,7)
>>> приблизительно
массив([[ 0. , 0. , 1. ],
[ 0,7 , 0, 0,96889112],
[1,38067777, 0, 0,87276349],
[2,00213905, 0, 0,7063497],
[2,5234414, 0, 0,45169729],
[2,66666667, 0, 0,33333333],
[-0,7 , 0, , 0,96889112],
[-1,38067777, 0. , 0,87276349],
[-2.00213905, 0. , 0.7063497 ],
[-2,5234414, 0, 0,45169729],
[-2,66666667, 0. , 0,33333333]])
>>> ellipse.plot(edgecolor='k', facecolor='none', lw=3)
>>> t = np.linspace(0, 2 * np.pi)
>>> для x, y, r примерно:
... plt.plot(x + r * np.cos(t), y + r * np.sin(t), 'b')
>>> plt.xticks(np.unique(np.concatenate((приблизительно[:, 0], (-3, 3)))))
>>> plt.yticks(np.unique(np.concatenate((приблизительно[:, 1], (-1, 1)))))
>>> plt.axis('в масштабе')
>>> plt.grid(True, linestyle=':')
>>> plt.show()
Выполнение приведенного выше кода приводит к рис. 28.
Рис. 28 Круговая аппроксимация эллипса по Ильину и Бернацкому.
- Параметры
x1 ( float или Нет ) – (опционально) Положение первого круга по оси +х.
 По умолчанию 0,5x самая короткая полуось.
По умолчанию 0,5x самая короткая полуось.- Возвращает
Список Nx3 данных (x, y, r) каждого круга приближение к эллипсу.
- Тип возврата
numpy.ndarray
- Поднимает
AssertionError — Выдается, если max(a, b) < x1.
- 1
Ильин, Д. Н., и Бернаки, М., «Алгоритм продвижения слоя упаковки плотного эллипса для генерации статистически эквивалентных Полигональные структуры», Granular Matter, vol. 18(3), стр. 43, 2016.
- classmethod area_expectation( **kwargs )[источник]
Ожидаемое значение площади.
Эта функция вычисляет ожидаемое значение площади эллипса. Аргументы ключевого слова такие же, как и входные параметры учебный класс. Значения ключевого слова могут быть либо константами (целые числа или числа с плавающей запятой), либо дистрибутивы из модуля SciPy
scipy. 2)\end{split}\] 9n \frac{A_i}{K_i}\end{split}\]
2)\end{split}\] 9n \frac{A_i}{K_i}\end{split}\], где \(n=1000\).
- Параметры
**kwargs – аргументы ключевого слова, см.
микроструктура.геометрия.Эллипс.- Возвращает
Ожидаемое значение площади эллипса.
- Тип возврата
поплавок
- best_fit( балла )[источник]
Найти эллипс, наиболее подходящий для точек
Эта функция вычисляет эллипс наилучшего соответствия набору точек. Он вызывает пакет подбора эллипса наименьших квадратов, который реализует опубликованный алгоритм подбора на Python. 2
Текущий экземпляр класса используется в качестве начального предположения для эллипс наилучшего соответствия. Так как эллипс может быть выражен кратно способами (например, повернуть на 90 градусов и перевернуть оси), это начальное предположение используется для выбора из нескольких наборов параметров.

- Параметры
точек ( список или numpy.ndarray ) — Nx2 список точек для соответствия.
- Возвращает
Экземпляр класса, который лучше всего соответствует точкам.
- Тип возврата
Эллипс
- 2
Халир, Р., Флюссер, Дж., «Численно стабильный прямой наименьший Квадраты, соответствующие эллипсам», 6-я Международная конференция в Центральной Европа по компьютерной графике и визуализации , Том. 98, 1998. (http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1.7559&rep=rep1&type=pdf)
- участок( **kwargs )[источник]
Постройте эллипс.
Эта функция добавляет исправление
matplotlib.patches.Ellipseв текущие оси с помощью matplotlib. Аргументы ключевого слова передаются в патч.- Параметры
**kwargs ( dict ) — Аргументы ключевых слов для matplotlib.

- отражение( точки )[источник]
Точки отражения на поверхности.
Эта функция отражает точку или набор точек на поверхности эллипса. Точки в центре эллипса не отражение.
- Параметры
точек ( список или numpy.ndarray ) — Nx2 список точек для отражения.
- Возвращает
Отраженные точки.
- Тип возврата
numpy.ndarray
- внутри( точки )[источник]
Проверить, находятся ли точки внутри эллипса.
Эта функция проверяет, находится ли точка или набор точек в эллипс. Для набора точек возвращается список логических значений. укажите, какие точки находятся внутри эллипса.
- Параметры
баллов ( список или numpy.ndarray ) — Точка или список точек.

- Возвращает
Установите значение True для точек в эллипсе.
- Тип возврата
bool или numpy.ndarray
- свойство angle_deg
Угол поворота, в градусах
- Тип
поплавок
- недвижимость угол_рад
Угол поворота, в радианах
- Тип
поплавок
- недвижимость площадь
Площадь эллипса, \(A = \pi a b\)
- Тип
поплавок
- свойство соотношение сторон
Отношение длины по оси X к длине по оси Y
- Тип
поплавок
- свойство оси
Список полуосей.
- Тип
кортеж
- свойство bound_max
Максимальная ограничивающая окружность эллипса, (x, y, r)
- Тип
кортеж
- свойство bound_min
Минимальная внутренняя окружность эллипса, (x, y, r)
- Тип
кортеж
- свойства ограничения
Список (нижняя, верхняя) границ ограничивающей рамки
- Тип
список
- свойство матрица
Матрица вращения
- Тип
numpy.
 ndarray
ndarray
- недвижимость n_dim
Количество размеров, 2
- Тип
инт
- свойство ориентация
Матрица вращения
- Тип
numpy.ndarray
- свойство sample_limits
Список (нижняя, верхняя) границ области выборки
- Тип
список
- свойство размер
Диаметр круга эквивалентной площади
- Тип
поплавок
- свойство объем
То же, что и
microstructpy.geometry.Ellipse.area- Тип
поплавок
SearchNeighborhoodSmooth—ArcGIS Pro | Документация
В этом разделе
- Сводка
- Синтаксис
- Свойства
- Пример кода
Сводка
Класс SearchNeighborhoodSmooth можно использовать для определения области поиска для IDW, локальной полиномиальной интерполяции и функций радиального базиса (только при использовании ключевого слова INVERSE_MULTIQUADRIC_FUNCTION). Класс окрестности гладкого поиска принимает входные данные для малой и большой осей, размера эллипса поиска, угла эллипса поиска и коэффициента сглаживания.
Класс окрестности гладкого поиска принимает входные данные для малой и большой осей, размера эллипса поиска, угла эллипса поиска и коэффициента сглаживания.
Learn more about smooth interpolation
Syntax
SearchNeighborhoodSmooth ({majorSemiaxis}, {minorSemiaxis}, {angle}, {smoothFactor}) | Parameter | Explanation | Data Type |
majorSemiaxis | Расстояние в единицах карты, определяющее длину большой полуоси эллипса, из которого выбираются данные. | Двойной |
minorSemiaxis | Расстояние в единицах карты, указывающее длину малой полуоси эллипса, из которого выбираются данные. | Двойной |
угол | Угол поискового эллипса. | Double |
smoothFactor | Определяет степень сглаживания. 0 — нет сглаживания; 1 — максимальная степень сглаживания. | Double |
Properties
| Property | Explanation | Data Type |
| angle (Read and Write) | The angle of the search ellipse. | Double |
| majorSemiaxis (чтение и запись) | Расстояние в единицах карты, указывающее длину большой полуоси эллипса, в пределах которого выбираются данные. | Double |
| minorSemiaxis (чтение и запись) | Расстояние в единицах карты, определяющее длину малой полуоси эллипса, в пределах которого выбираются данные. | Double |
| nbrType (только чтение) | Тип соседства: Гладкий или Стандартный. | String |
| smoothFactor (чтение и запись) | Определяет степень сглаживания: 0 означает отсутствие сглаживания, 1 максимальное количество сглаживания. | Double |
Пример кода
SearchNeighborhoodSmooth (окно Python)SearchNeighborhoodSmooth с локальной полиномиальной интерполяцией для создания выходного растра.
импорт аркпи
arcpy.env.workspace = "C:/gapyexamples/data"
arcpy.LocalPolynomialInterpolation_ga(
"ca_ozone_pts", "OZONE", "outLPI", "C:/gapyexamples/output/lpiout", "2000",
"2", arcpy.SearchNeighborhoodSmooth(300000, 300000, 0, 0.5), "QUARTIC",
"", "", "", "", "ПРОГНОЗ") SearchNeighborhoodSmooth (автономный скрипт) SearchNeighborhoodSmooth с локальной полиномиальной интерполяцией для создания выходного растра.
# Имя: LocalPolynomialInterpolation_Example_02.py
# Описание: Локальная полиномиальная интерполяция подходит ко многим полиномам, каждый из которых
# в указанных перекрывающихся районах.
# Требования: расширение Geostatistical Analyst
# Импорт системных модулей
импортировать аркпи
# Установить параметры среды
arcpy.env.workspace = "C:/gapyexamples/data"
# Установить локальные переменные
inPointFeatures = "ca_ozone_pts.shp"
zField = "озон"
выходной слой = "выходной ЛПИ"
outRaster = "C:/gapyexamples/output/lpiout"
размер ячейки = 2000,0
сила = 2
функция ядра = "КВАРТИК"
пропускная способность = ""
использоватьConNumber = ""
конномер = ""
поле веса = ""
outSurface = "ПРОГНОЗ"
# Установить переменные для поиска окрестности
majSemiaxis = 300000
минполуоси = 300000
угол = 0
SmoothFactor = 0,5
searchNeighbourhood = arcpy.SearchNeighborhoodSmooth(majSemiaxis, minSemiaxis,
угол, SmoothFactor)
# Выполнить локальную полиномиальную интерполяцию
arcpy. LocalPolynomialInterpolation_ga(inPointFeatures, zField, outLayer, outRaster,
размер ячейки, мощность, searchNeighbourhood,
функция ядра, пропускная способность, useConNumber,
conNumber, weightField, outSurface)
LocalPolynomialInterpolation_ga(inPointFeatures, zField, outLayer, outRaster,
размер ячейки, мощность, searchNeighbourhood,
функция ядра, пропускная способность, useConNumber,
conNumber, weightField, outSurface) Отзыв по этой теме?
Как мне узнать, что такое a и b?
Расчетный интеграл объема
Диана Р.
спросил 10.07.21Установите интеграл, вычисляющий объем конуса высотой 12, основанием которого является эллипс с большой полуосью 6 и малой полуосью 4. Формула площади эллипса: pi(a)(b) , где a — длина большой полуоси и b – длина малой полуоси.
Подписаться І 2
Подробнее
Отчет
3 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшиеНовостиСамые старые
Жилберто С. ответил 10.07.21
ответил 10.07.21
Репетитор
92 / 6 дхГолосовать за 1 Понизить
Подробнее
Отчет
Адам Б. ответил 10.07.21
Репетитор
5,0 (269)
«Молодой» профессор математики, недавно вышедший на пенсию
Об этом репетиторе ›
Об этом репетиторе ›
Теперь, если бы проблема была просто базовой задачей геометрии, вычисление объема конуса было бы
легко найти, поскольку V = 1/3 (площадь основания) (высота) = (1/3) (π ⋅6⋅4)⋅12 = 96 π кубических единиц
Но нам нужно использовать исчисление, чтобы получить тот же результат.
.
Введем прямоугольную систему координат, в которой ось x проходит через вершину конуса.
перпендикулярен основанию и проходит через центр эллипса эллиптического основания.
Также вершина конуса находится в начале координат
При любом x в интервале [0,12] на оси x поперечное сечение, перпендикулярное оси x, представляет собой эллипс, подобный эллипсу основания конуса.
Если мы обозначим через A площадь эллипса, а через A x площадь перпендикулярного среза конуса в точке x
по оси x, то, используя подобие
A / A x = ( 12 / x ) 2 (см. сноску)
Затем A x = (x/ 12) 2 A
⋅a x = (x/ 12) 2 ⋅π = 6t4
⋅a x = (x/ 12)
1 22 2 2. ⋅24πA x = πt x 2 /6
, а объем V из конуса -
V = ∫ 12 0 A x DX x
Примечание: когда геометрические фигуры подобны, отношение их площадей равно квадрат их
степень сходства.
Голосовать за 0 Понизить
Подробнее
Отчет
Катя С. ответил 10.07.21
Репетитор
5,0 (82)
Пре-/Алгебра, Триггеры, Пре-/Исчисление, Геометрия. ИТ и русский язык.
Об этом репетиторе ›
Об этом репетиторе ›
Диана, напиши мне сообщение, чтобы я мог послать тебе изображение правильной установки конуса, которое ты будешь использовать, чтобы установить сумму Реймана, а затем получить интеграл, который ты сможешь использовать для вычисления объема.
Вы устанавливаете свой нижний уровень как «ноль», затем берете небольшой кусочек конуса. Объем среза будет равен ∆h *π*α*β, где дельта-h — высота этого цилиндра, а альфа и бетта — соответствующие оси этого «разреза».



 Р. Динамическая образовательная среда GeoGebra / А.Р. Есаян, Н.М. Добровольский, Е.А. Седова, А.В. Якушин– Тула: Извд-во Тул.гос.пед.ун-та им. Л.Н.Толстого, 2017. – Ч.1. – 417 с.
Р. Динамическая образовательная среда GeoGebra / А.Р. Есаян, Н.М. Добровольский, Е.А. Седова, А.В. Якушин– Тула: Извд-во Тул.гос.пед.ун-та им. Л.Н.Толстого, 2017. – Ч.1. – 417 с. Информатика. – 2017. – № 2 (23). – С. 71-84.
Информатика. – 2017. – № 2 (23). – С. 71-84. L. Obuchenie geometrii s ispol`zovaniem vozmozhnostej GeoGebra [Teaching geometry using GeoGebra] / Bezumova O.L., Ovchinnikova R.P. et al. Arxangel`sk, Publishing house OOO «Kira», 2011. – 140 p. [in Russian]
L. Obuchenie geometrii s ispol`zovaniem vozmozhnostej GeoGebra [Teaching geometry using GeoGebra] / Bezumova O.L., Ovchinnikova R.P. et al. Arxangel`sk, Publishing house OOO «Kira», 2011. – 140 p. [in Russian]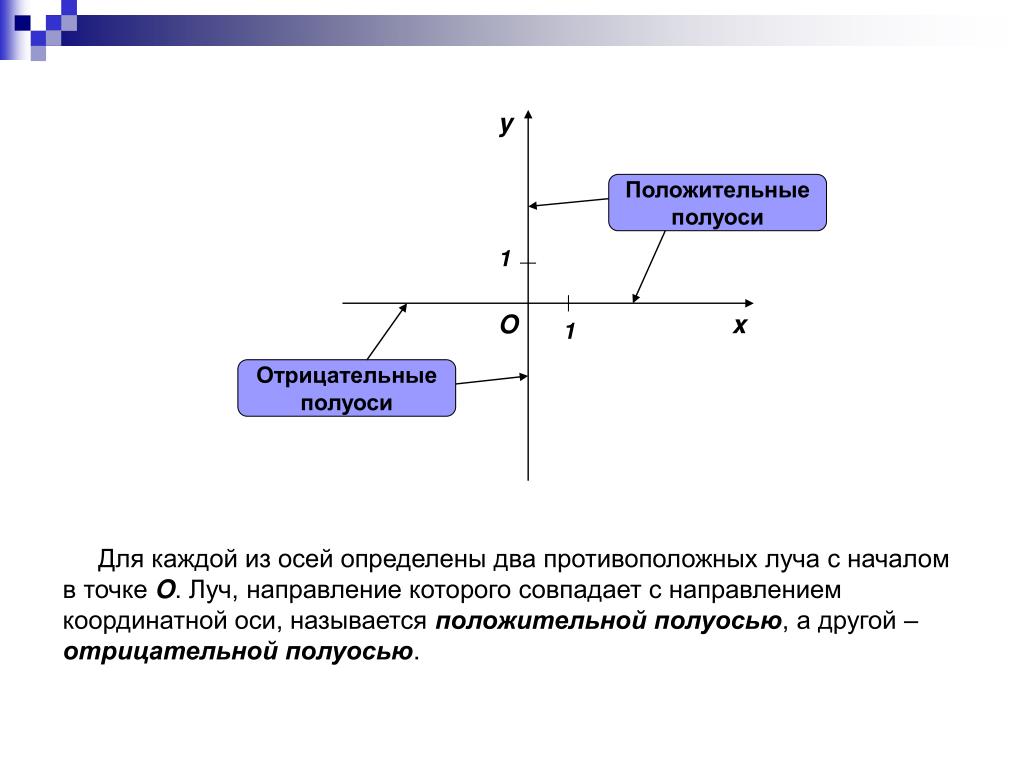 A. Zaslavskii. – M.: MCzMNO, 2004. – 86 p. [in Russian]
A. Zaslavskii. – M.: MCzMNO, 2004. – 86 p. [in Russian] – 2017. — № 2 (23). – p. 71-84. [in Russian]
– 2017. — № 2 (23). – p. 71-84. [in Russian]


 приблизительно(0,7)
>>> приблизительно
массив([[ 0. , 0. , 1. ],
[ 0,7 , 0, 0,96889112],
[1,38067777, 0, 0,87276349],
[2,00213905, 0, 0,7063497],
[2,5234414, 0, 0,45169729],
[2,66666667, 0, 0,33333333],
[-0,7 , 0, , 0,96889112],
[-1,38067777, 0. , 0,87276349],
[-2.00213905, 0. , 0.7063497 ],
[-2,5234414, 0, 0,45169729],
[-2,66666667, 0. , 0,33333333]])
>>> ellipse.plot(edgecolor='k', facecolor='none', lw=3)
>>> t = np.linspace(0, 2 * np.pi)
>>> для x, y, r примерно:
... plt.plot(x + r * np.cos(t), y + r * np.sin(t), 'b')
>>> plt.xticks(np.unique(np.concatenate((приблизительно[:, 0], (-3, 3)))))
>>> plt.yticks(np.unique(np.concatenate((приблизительно[:, 1], (-1, 1)))))
>>> plt.axis('в масштабе')
>>> plt.grid(True, linestyle=':')
>>> plt.show()
приблизительно(0,7)
>>> приблизительно
массив([[ 0. , 0. , 1. ],
[ 0,7 , 0, 0,96889112],
[1,38067777, 0, 0,87276349],
[2,00213905, 0, 0,7063497],
[2,5234414, 0, 0,45169729],
[2,66666667, 0, 0,33333333],
[-0,7 , 0, , 0,96889112],
[-1,38067777, 0. , 0,87276349],
[-2.00213905, 0. , 0.7063497 ],
[-2,5234414, 0, 0,45169729],
[-2,66666667, 0. , 0,33333333]])
>>> ellipse.plot(edgecolor='k', facecolor='none', lw=3)
>>> t = np.linspace(0, 2 * np.pi)
>>> для x, y, r примерно:
... plt.plot(x + r * np.cos(t), y + r * np.sin(t), 'b')
>>> plt.xticks(np.unique(np.concatenate((приблизительно[:, 0], (-3, 3)))))
>>> plt.yticks(np.unique(np.concatenate((приблизительно[:, 1], (-1, 1)))))
>>> plt.axis('в масштабе')
>>> plt.grid(True, linestyle=':')
>>> plt.show()
 По умолчанию 0,5x самая короткая полуось.
По умолчанию 0,5x самая короткая полуось. 2)\end{split}\] 9n \frac{A_i}{K_i}\end{split}\]
2)\end{split}\] 9n \frac{A_i}{K_i}\end{split}\]