(1)
Если пренебречь краевыми эффектами, то первое и третье слагаемые в (1) будут равны нулю, так как магнитное поле перпендикулярно контуру и $B_l=0$. Если контур выбрать так, что $AD$ будет лежать на большом расстоянии от соленоида, где поле стремиться к нулю, то и четвёртое слагаемое в (1) также превратиться в нуль. Тогда, учитывая приближение однородности поля получим:
\[B_l L=\mu_0 NI,\]
(2)
где $L$ – длина соленоида, $N$ – количество витков. Если ввести понятие плотности витков (число витков на единицу длины) $n=N/L$, то индукцию магнитного поля внутри соленоида (2) можно записать в виде:
\[B=\mu_0 nI.\]
(3)
Рис. 2: Соленоид с произвольными размерами $L$ и $R$.
Чтобы получить точное выражение для индукции магнитного поля в любой точке на оси конечного соленоида необходимо воспользоваться законом Био-Савара-Лапласа (Рис. 2), который приводит к следующему выражению:
\[B=\frac12\mu_0 nI (\cos\alpha_2-\cos\alpha_1).
2}},\]
(5)
где $R$ – радиус соленоида. А на краю полубесконечного соленоида:
\[B=\frac12 \mu_0 nI.\]
(6)
Индукция магнитного поля бесконечного соленоида (3)
Плотность намотки n (м-1)
Сила тока соленоида I (A)
B = Тл
Индукция магнитного поля конечного соленоида (5)
Плотность намотки n (м-1)
Радиус намотки R (м)
Длина соленоида L (м)
Сила тока соленоида I (A)
B = Тл
Распределение индукция магнитного внутри конечного соленоида (4)
Плотность намотки n (м-1)
Радиус намотки R (м)
Длина соленоида L (м)
Сила тока соленоида I (A)
Электричество и магнетизм
|
Соленоидом называется цилиндрическая катушка, состоящая из большого числа витков провода, образующих винтовую линию (рис. |
6.23-1).
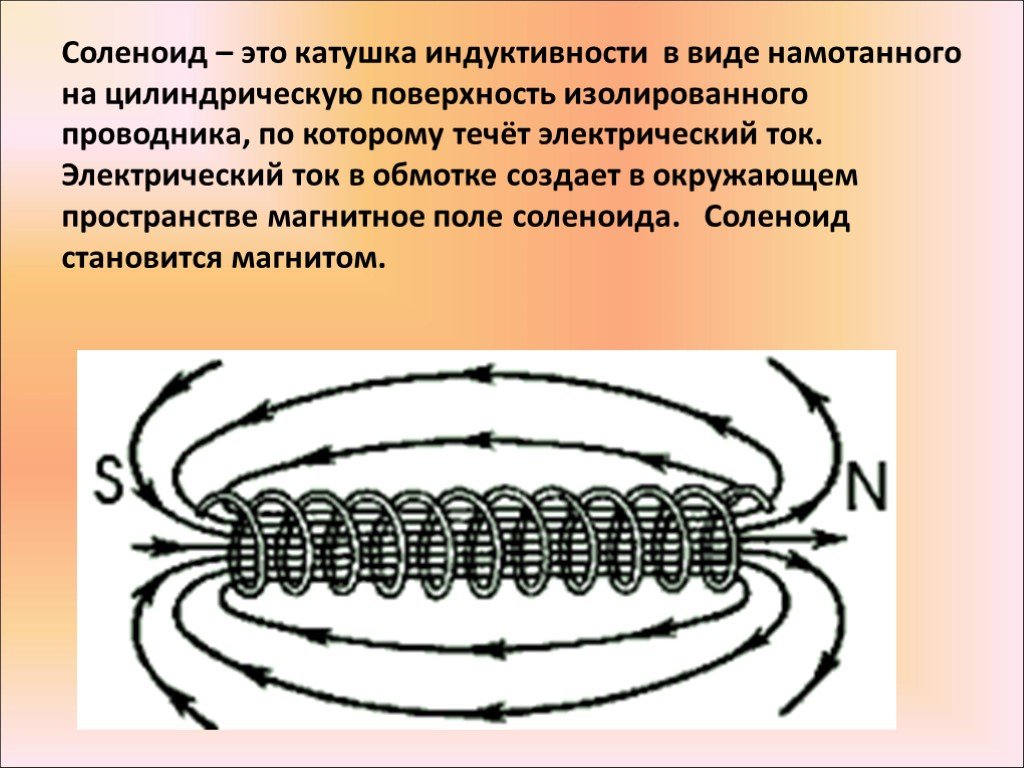
Рис. 6.23. Магнитные силовые линии поля: 1 — соленоида; 2 — полосового магнита
Магнитное поле соленоида напоминает поле полосового магнита (рис. 6.23-2).
Если витки намотаны вплотную, то соленоид — это система круговых токов, имеющих одну ось.
Если считать соленоид достаточно длинным, то магнитное поле внутри соленоида однородно и направлено параллельно оси. Вне соленоида вдали от краев магнитное поле также должно иметь направление параллельное оси и на большом расстоянии от соленоида должно быть очень слабым. Поле убывает по закону
Подсчитаем поле внутри соленоида. Возьмем элемент соленоида длиной dh, находящийся на расстоянии h от точки наблюдения. Если катушка имеет n витков на единицу длины, то в выделенном элементе содержится ndh витков. Согласно формуле (6.11), этот элемент создает магнитное поле
|
(6. |
Интегрируя по всей длине соленоида, получаем
|
(6.19) |
Таким образом, поле в бесконечно длинном соленоиде дается выражением
|
|
(6.20) |
На практике соленоиды бесконечно длинными не бывают. Для иллюстрации рассмотрим некоторые примеры.
Пример 1. Найти магнитное поле в середине соленоида конечной длины l (рис. 6.24). Сравнить с полем бесконечно длинного соленоида. При каких условиях разница составляет менее 0,5 %?
Рис. 6.24. Магнитное поле катушки конечной длины
В центре соленоида магнитное поле практически однородно и значительно превышает по модулю поле вне катушки
Решение.
Магнитное поле в средней точке оси соленоида конечной длины l дается тем же интегралом (6.19), но с другими пределами интегрирования
|
(6.21) |
Если длина соленоида много больше его диаметра (l >> 2R), мы возвращаемся к формуле для поля в бесконечно длинном соленоиде (6.20). Относительная разница этих двух значений равна
По условию эта разница мала: , то есть мало отношение диаметра соленоида к его длине: 2R/l << 1. Поэтому можно воспользоваться формулой разложения квадратного корня
Отсюда
или
Подставляя численное значение d, находим, что разница будет менее половины процента при выполнении соотношения
Иными словами, соленоид может рассматриваться как бесконечно длинный, если его длина в двадцать или более раз превышает радиус.
Пример 2. Найти магнитное поле Ве в крайней торцевой точке оси соленоида конечной длины l. Сравнить с результатом предыдущего примера.
Решение. Магнитное поле в торцевой точке оси соленоида конечной длины l дается тем же интегралом (6.19), но теперь пределы интегрирования будут выглядеть иначе
|
(6.22) |
Отношение полей в средней и крайней точках оси соленоида равно
Это отношение всегда меньше единицы (то есть поле на торце меньше поля в середине соленоида). При l >> R имеем
Этот результат легко понять. Представим себе бесконечный соленоид, который мысленно рассекаем пополам в точке наблюдения. Можно считать, что поле в этой точке создается двумя одинаковыми «полубесконечными» соленоидами, расположенными по разные стороны от нее.
Ясно, что при удалении одного из них точка наблюдения становится торцом оставшегося «полубесконечного» соленоида, а магнитная индукция в ней уменьшиться именно в два раза.
Это — так называемый краевой эффект. Пример демонстрирует, что недостаточно выполнения соотношения l >> R, чтобы пользоваться формулами для бесконечно длинного соленоида; надо еще, чтобы точка наблюдения находилась далеко от его концов.
На рис. 6.25 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг соленоида. Поле соленоида, ось которого лежит в плоскости пластинки, сосредоточено в основном внутри соленоида. Силовые линии внутри имеют вид параллельных прямых вдоль оси катушки, а поле снаружи практически отсутствует.
Рис. 6.25. Визуализация силовых линий магнитного поля
Видео 6.1. Силовые линии магнитного поля проводников с током различной формы: прямой ток, соленоид, один виток.
Соленоидыкак источники магнитного поля Соленоиды
как источники магнитного поля Длинная прямая катушка проволоки может быть использована для создания почти однородного магнитного поля, подобного магнитному стержню. В приведенном выше выражении для магнитного поля B n = N/L — это число витков на единицу длины, иногда называемое «плотностью витков». Магнитное поле B пропорционально току I в катушке. Выражение представляет собой идеализацию соленоида бесконечной длины, но дает хорошее приближение к полю длинного соленоида.
| Индекс Концепции магнитного поля Токи как источники магнитного поля | ||||||||||||||||||||||||||
|
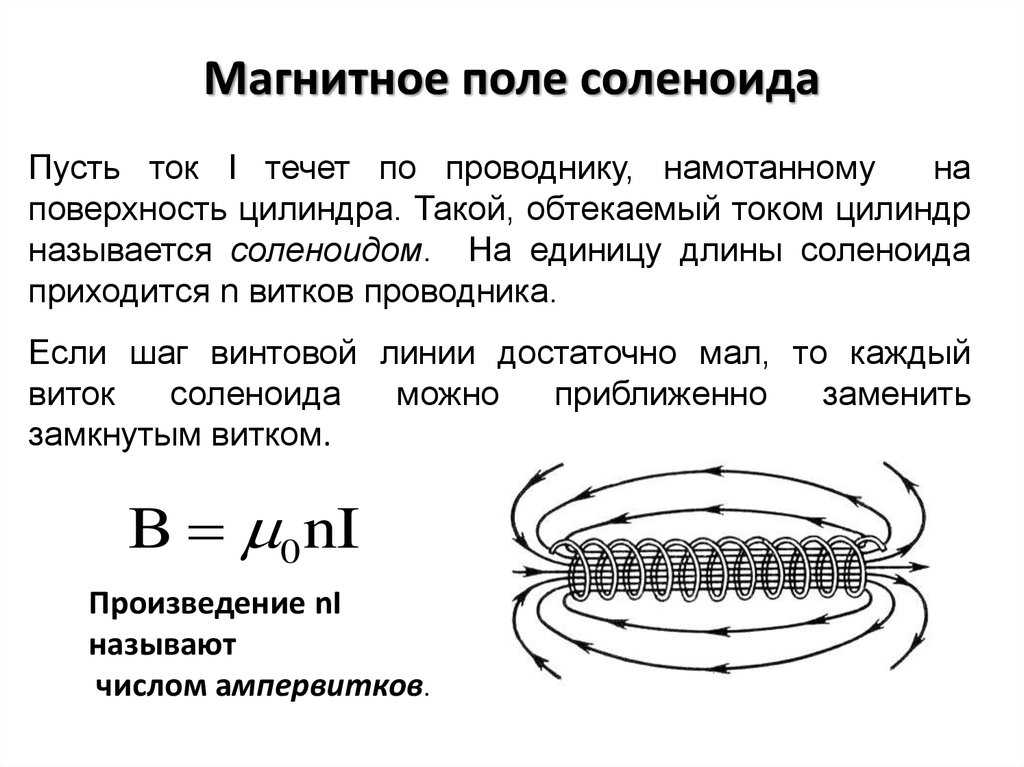
Поле
по сути
перпендикулярно
стороны
путь, давая
незначительный
вклад. Если
конец взят до сих пор
от катушки, которая
поле пренебрежимо мало, то
длина внутри катушки
является доминирующим вкладом.
Эта статья даст вам некоторое представление о соленоидах: как они работают и для чего используются.
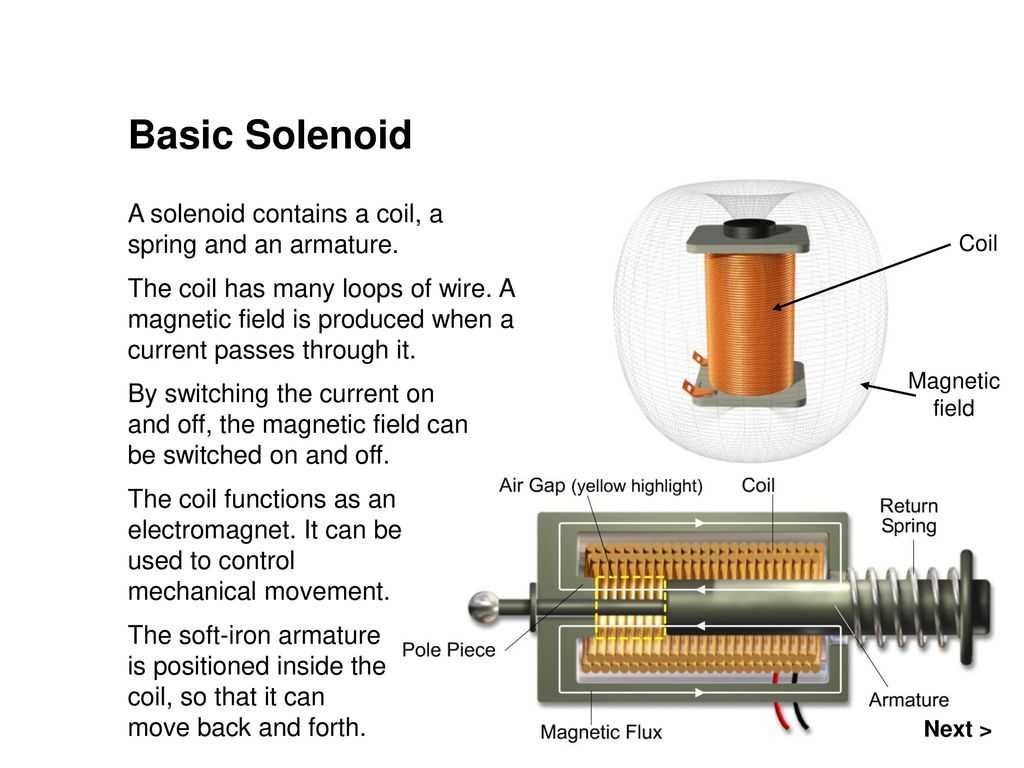
Он также используется в качестве интерфейса, соединяющего пневматическую систему и управляющие ими электронные контроллеры. Гидравлические соленоиды. По функциям аналогичны пневматическим соленоидам, основное отличие состоит в том, что гидравлические соленоиды управляют потоком жидкости, обычно масла. Этот тип соленоида обычно используется для контроля количества масла, используемого в автоматизированном оборудовании для изготовления металлов. Они также используются для управления потоком трансмиссионной жидкости в автоматических коробках передач. Соленоиды стартера. Используемые в автомобилях соленоиды стартера, иногда называемые реле стартера, являются частью системы зажигания. При повороте ключа напряжение от аккумулятора и замка зажигания приводит к замыканию соленоида, что приводит к запуску двигателя. Когда у кого-то разряжен аккумулятор, и они пытаются завести машину, они слышат щелкающий звук, исходящий от соленоида стартера.