крутящий момент- Что такое крутящий момент для электроинструмента
Что, черт возьми, люди имеют в виду, когда говорят о величине крутящего момента или настройках крутящего момента?Чтобы помочь разоблачить жаргон инструментов, мы расскажем вам об основах настройки крутящего момента, о том, почему это важно и когда вам нужно будет использовать его, чтобы дать вам возможность сделать правильный выбор при следующей покупке инструмента.
1 🔰 Что означает установка крутящего момента?
2 🔰 Действительно Ли Крутящий Момент Имеет Значение?alte moshabeh
3 🔰 Ньютон-метры (Нм) на сверлах:
Что, черт возьми, люди имеют в виду, когда говорят о величине крутящего момента или настройках крутящего момента?Чтобы помочь разоблачить жаргон инструментов, мы расскажем вам об основах настройки крутящего момента, о том, почему это важно и когда вам нужно будет использовать его, чтобы дать вам возможность сделать правильный выбор при следующей покупке инструмента.
Крутящий момент — это сила вращения, создаваемая коленчатым валом электродвигателя.
С широким диапазоном крутящего момента на инструменте для практически неограниченного применения может быть сложно найти оборудование, подходящее для ваших нужд.
Крутящий момент, измеряемый в ньютон-метрах (Нм), — это сила, которая заставляет объект вращаться, и это лучший показатель, позволяющий определить, насколько мощна ваша дрель или ударный привод, и чем больше число в ньютон-метрах, тем большую крутящую силу он будет оказывать.
🔰 Что означает установка крутящего момента?
Величина крутящего момента фактически указывает мощность, которую ваше устройство должно использовать для преобразования электрического тока в циркулирующий ток. Контроль крутящего момента на электроинструменте относится к мощности циркуляции.
Подумайте о настройках крутящего момента, таких как сцепление в автомобиле. Когда вы нажимаете на педаль сцепления до упора, колеса автомобиля теряют мощность и скорость. Когда вы отпускаете педаль сцепления, вся мощность передается колесам, и они вращаются быстрее.
Когда вы отпускаете педаль сцепления, вся мощность передается колесам, и они вращаются быстрее.
Спусковой крючок на дрели действует как педаль акселератора в автомобиле, чем сильнее вы нажимаете на спусковой крючок, тем быстрее вращается дрель.
Настройки крутящего момента на дрелиВы можете задаться вопросом: «Зачем мне когда-либо хотеть, чтобы мой электроинструмент был менее мощным?»
Правда в том, что есть ряд случаев, когда вы, возможно, захотите уменьшить крутящий момент, чтобы дать себе больше контроля. Переменные настройки крутящего момента делают вашу дрель более универсальной и позволяют выполнять более широкий спектр работ с помощью одного и того же электроинструмента.
Стоит помнить, что вы просто не можете использовать величину крутящего момента, чтобы решить, какой электроинструмент лучше. Тот, который имеет относительно низкий уровень крутящего момента, все равно может быть быстрее или работать лучше, чем сверло с высоким крутящим моментом, если остальные характеристики будут лучше.
Сказав это, имеет смысл понять эффект, который оказывает крутящий момент.
Например, когда вы используете Аккумуляторную дрель или шуруповерт, возможно, вы заметили циферблат рядом с головкой сверла с различными цифрами или символами на нем. Если да, то вы, вероятно, задавались вопросом: “Какие разные цифры/символы на беспроводной дрели и что они означают?
Цифры на Аккумуляторной дрели указывают точку разрыва крутящего момента или мощность вращения. Чем больше число, тем больше сила или крутящий момент. Эта функция очень полезна. Он не только позволяет регулировать мощность поворота, применяемую для предотвращения срыва винтов, но также обеспечивает возможность сверления отверстий в твердых материалах, таких как дерево, бетон, каменная кладка и металл.
Крутящий момент сверла — это величина силы, которую оно способно приложить. Чем выше крутящий момент, тем легче он сможет выполнять даже самые сложные работы.
Обычно вы увидите эти классы силы в дюймах-фунтах. Самые мощные аккумуляторные дрели могут дать вам измерения до 1000, что является огромным усилием.
🔰 Действительно Ли Крутящий Момент Имеет Значение?alte moshabeh
На этом этапе вы можете задаться вопросом, насколько важен для вас высокий уровень крутящего момента. Первый момент, который следует учитывать, — это то, в какой материал вы собираетесь сверлить.
Если вы в основном собираетесь работать с деревом, крутящий момент не будет большой проблемой. Даже сверла с самым низким уровнем крутящего момента не будут слишком сильно сопротивляться сверлению в древесине.
Настройки крутящего моментаС другой стороны, если вы собираетесь работать с более жесткими материалами, крутящий момент будет играть большую роль в процессе принятия решений. Это не единственный вопрос, который следует учитывать, но вы будете чувствовать себя более комфортно, берясь за большую работу, когда у вас будет мощная аккумуляторная дрель, на которую вы можете положиться.
При закручивании винтов, чем тверже материал, тем меньшая скорость и больший крутящий момент вам, вероятно, понадобятся. Правильное выполнение этих настроек поможет вам контролировать глубину бурения без причинения какого-либо ущерба.
Правильное выполнение этих настроек поможет вам контролировать глубину бурения без причинения какого-либо ущерба.
При сверлении отверстий, чем тверже материал, тем выше скорость для получения наилучшего результата.
Товары из категорий 🛠
🔰 Ньютон-метры (Нм) на сверлах:
От 4 до 15 Нм подходит для всех этих небольших задач отвертки по дому.
От 15 до 35 Нм — отличный универсальный электроинструмент для сверления и привода винтов средних размеров и сверления отверстий.
35 Нм вверх будет решать все эти более серьезные проекты с большими винтами и отверстиями.
Непременно учитывайте величину крутящего момента при выборе нового электроинструмента. Однако не совершайте ошибку, думая, что это единственная проблема, о которой вам нужно знать.
Большинство проектов DIY не потребуют от вас огромного количества энергии или крутящего момента для успешного выполнения домашних задач. Большинство качественных аккумуляторных дрелей от известных брендов оснащены настройками переменной скорости, яркой светодиодной подсветкой и функцией перфоратора.
В то время как мощность, скорость и крутящий момент — это сексуальные показатели, на которые каждый хочет обратить внимание при покупке лучшей аккумуляторной дрели. Дело в том, что самая мощная беспроводная дрель не всегда является лучшим инструментом для вас. Покупайте инструмент, который лучше всего подходит для вас, а не то, что считается лучшим статистически.
Заключение🧾
При покупке лучшего электроинструмента каждый обратит внимание на мощность, скорость и крутящий момент. Дело в том, что самая мощная аккумуляторная дрель — не всегда лучший инструмент для вас. Купите инструмент, который лучше всего подходит для вас, а не тот, который считается лучшим по статистике.
Как измерять крутящий момент? | Dewesoft
Автор: Грант Малой Смит (Grant Maloy Smith), специалист по сбору данных
Данная статья об измерении крутящего момента поможет вам:
- Понять, что такое крутящий момент
- Узнать, как измерять крутящий момент
- Ознакомиться со спецификой измерения крутящего момента при сборе данных
Что такое крутящий момент?
Если вы не пропускали уроки физики в школе, то помните, что сила — это воздействие, приводящее тело в движение в течение времени.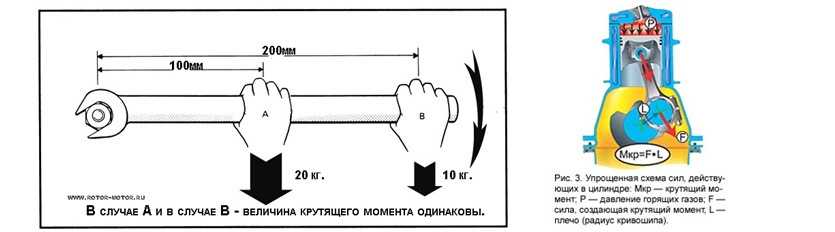 Например, простое линейное усилие может толкнуть (или притянуть) массу в состоянии покоя и изменить её скорость путём ускорения. Крутящий момент — сила, которая вызывает вращение тела по своей оси вращения. Так, крутящий момент — это крутящее усилие, которое называют вращающей силой.
Например, простое линейное усилие может толкнуть (или притянуть) массу в состоянии покоя и изменить её скорость путём ускорения. Крутящий момент — сила, которая вызывает вращение тела по своей оси вращения. Так, крутящий момент — это крутящее усилие, которое называют вращающей силой.
Наиболее очевидный пример крутящего момента — приводной вал автомобиля. Вызываемый двигателем крутящий момент вала приводит автомобиль в движение. Крутящий момент — это вектор: это означает, что он имеет направление.
Крутящий момент — усилие, вращающее или поворачивающее приводной вал, винт или колесо.
Вращающее усилие
Также крутящий момент называют моментом или моментом силы. Как правило, крутящий момент обозначают символом $τ$ (греческой буквой «т»). Единица измерения крутящего момента по системе СИ — $N\cdot m$ (Н·м).
В США для его выражения используют футо-фунты ($ft/lbs$). Для перевода $N\cdot m$ в $ft/lbs$ достаточно разделить $N\cdot m$ на 1,356.
Старшина второй статьи Джеймс Р. Эванс (James R. Evans) осматривает приводной вал хвостового винта вертолёта ВМС США. Снимок из открытого доступа, Wikimedia Commons
Для чего измеряют крутящий момент?
Измерение механического крутящего момента торсионных валов — важнейший этап проектирования и сбора различных машин, а также устранения их неисправностей. Истинное значение механического крутящего момента вала, пропеллера или другого вращающегося компонента — единственный способ понять, отвечает ли он требованиям.
В некоторых случаях крутящий момент необходимо отслеживать постоянно: например, чтобы предотвратить потенциально опасный чрезмерный крутящий момент, который может привести к выходу системы из строя. Также измерения крутящего момента играют важную роль при диагностическом техническом обслуживании.
Какие виды крутящего момента существуют?
Крутящий момент делится на два вида: вращающий и реактивный:
- вращающий — то есть вращающий или динамический крутящий момент;
- реактивный — то есть стационарный или статичный крутящий момент.

Вращающий момент
Тела, которые многократно (или постоянно) вращаются вокруг своей оси (например, валы, турбины, колёса), имеют вращающий момент.
Реактивный момент
Воздействующая на тело статичная сила называется реактивным крутящим моментом. Например, при попытке закрутить болт ключом на болт воздействует реактивная сила. Такая сила воздействует даже тогда, когда болт не крутится. В таких случаях крутящий момент измеряют не за полный оборот.
Как измеряется крутящий момент?
Крутящий момент можно измерить косвенно или напрямую. Если известны КПД двигателя и скорость вала, с помощью измерителя мощности можно вычислить крутящий момент. Такое измерение называют косвенным.
Более точным методом является прямое измерение крутящего момента с помощью датчиков крутящего момента или роторных моментомеров. Чем они отличаются?
Датчики реактивного (статичного) крутящего момента
Датчик Torquemaster. CC BY-SA 3.0, Wikimedia Commons
Датчик реактивного крутящего момента измеряет статический крутящий момент.
Пример датчика крутящего момента — динамометрический ключ. С помощью таких ключей можно точно измерить крутящий момент, прилагаемый к болту, гайке или другому креплению. В основании ключа можно задать нужный крутящий момент, после чего при затягивании крепления оператором до нужного момента раздастся щелчок. Как правило, такие ключи называют щелчковыми. На них можно задать несколько значений момента.
Цифровые динамометрические ключи оснащены иглой или цифровым дисплеем, на котором отображается прилагаемое усилие. Ряд электронных моделей (в частотности промышленных) имеют память, в которой хранится каждое измерение значение (для ведения документации или контроля качества).
Принцип работы щелчкового динамометрического ключа продемонстрирован в следующем видео:
В основе датчика реактивного крутящего момента лежит кварцевый пьезоэлектрический датчик или тензодатчик. Сегодня на рынке представлены различные виды и конфигурации динамометрических ключей и отвёрток.
Сегодня на рынке представлены различные виды и конфигурации динамометрических ключей и отвёрток.
Датчики крутящего момента
Датчик крутящего момента — это преобразователь, который преобразовывает вращающий момент в сигнал, который можно измерить, проанализировать, отобразить и сохранить. Преобразователи крутящего момента применяются для испытаний крутящего момента двигателя, испытаний ДВС, испытаний электродвигателей, валов, турбин, генераторов и т.д.
Измерить крутящий момент можно как напрямую, так и косвенно.
Косвенное измерение крутящего момента — более экономичный и удобный метод измерения, точность которого уступает методу прямого измерения. Он подходит для случаев, когда известен КПД двигателя и имеется возможность измерить скорость вала и расход тока.
Прямое измерение — более точный способ. Для прямого измерения на вале закрепляют тензодатчик, который измеряет крутящее усилие на вале.
На вале закрепляют тензодатчик.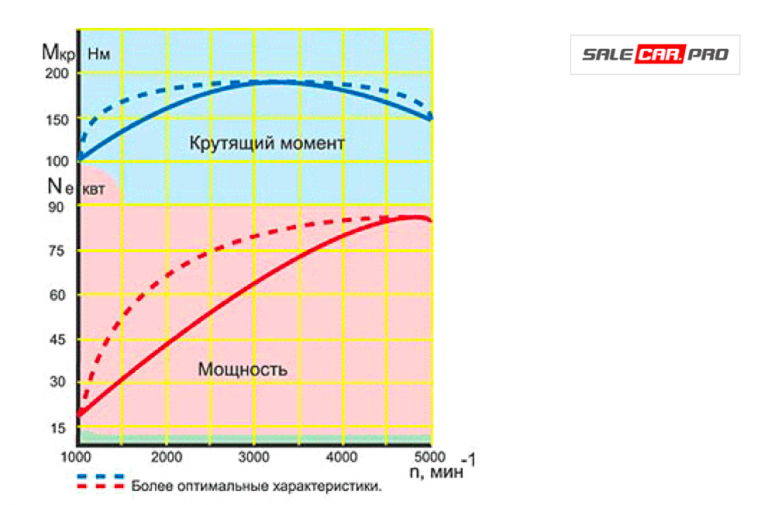 Вращательное усилие заставляет вал вращаться.
Вращательное усилие заставляет вал вращаться.
При повороте вала двигателем вращательное усилие будет незначительным. Из-за жёсткости стали увидеть вращение нельзя, однако его можно считать с помощью закреплённых на вале тензодатчиков. Четыре датчика образуют мост Уитстона, выход которого балансируется и нормируется системой измерения крутящего момента.
Выход тензодатчика можно передать по проводу (если возможно) или дистанционно на систему измерения крутящего момента или систему сбора данных.
Стандартная система измерения крутящего момента
Внутри датчика крутящего момента выходы закреплённых на вале тензодатчиков передаются на электронные компоненты по контактному кольцу (на тензодатчики должно подаваться питание). Также можно подключить бесщёточный или индуктивный датчик: он повышает скорость и меньше изнашивается, а значит требует меньшего технического обслуживания. Бесконтактным способом можно измерить угол и частоту вращения.
Системы сбора данных Dewesoft — идеальные решения для измерения любых физических параметров, в том числе крутящего момента. В них встроены изолированные блоки преобразования сигналов, которые сокращают количество шумов и гарантируют высокую точность данных. Также они имеют входы счётчика, частоты вращения и энкодера, а значит подходят для одновременного измерения скорости, угла и положения вала. В системах сбора данных данные с аналоговых и цифровых счётчиков полностью синхронизированы между собой, и этот фактор играет важную роль при решении любых задач, особенно при испытании вибрации кручения и вращения. Подробнее об этом — в следующем разделе.
В них встроены изолированные блоки преобразования сигналов, которые сокращают количество шумов и гарантируют высокую точность данных. Также они имеют входы счётчика, частоты вращения и энкодера, а значит подходят для одновременного измерения скорости, угла и положения вала. В системах сбора данных данные с аналоговых и цифровых счётчиков полностью синхронизированы между собой, и этот фактор играет важную роль при решении любых задач, особенно при испытании вибрации кручения и вращения. Подробнее об этом — в следующем разделе.
Испытание вибрации кручения и вращения в ПО Dewesoft X
Стационарные системы измерения крутящего момента
В представленной выше системе датчик крутящего момента закреплён между двигателем и тормозом с помощью соединений с каждой стороны. Проходящий через вал датчик оснащен тензодатчиком, который измеряет крутящее усилие вала. После преобразования выход сигнала отправляется на систему сбора данных, цифровой дисплей или аварийную систему (при мониторинге, а не записи данных).
При необходимости датчики крутящего момента можно оснастить энкодером, который точно выводит скорость и угол вала. Такие выводы применяют для анализа вибрации кручения и вращения. Выводы скорости и угла крайне важны при использовании динамометров для вычисления выходной мощности (выраженной в $HP$ или $Kw$) и КПД двигателя.
Портативные системы измерения крутящего момента
Для временных измерений крутящего момента тензодатчики можно закрепить на приводном вале. Компактный интерфейс с питанием от аккумулятора питает датчики и дистанционно передаёт данные на ближайший блок преобразования, в котором с помощью системы сбора данных их можно записать, отобразить или проанализировать.
Беспроводной датчик крутящего момента. Изображение предоставлено компанией Parker-LORD MicroStrain Sensing
Беспроводные датчики Parker-Lord совместимы с ПО Dewesoft X: их можно объединить с системами сбора данных и использовать на неограниченном количестве каналов.
Области применения порядкового анализа
Вибрации кручения могут стать причиной выхода торсионных валов из строя. Анализ вибрации вращения и кручения — важный способ устранения неисправностей валов, коленчатых валов и зубчатых передач в автомобилестроении, промышленности и в производстве электроэнергии.
Что такое вибрация кручения?
Вибрации кручения — угловые вибрации тела (как правило, вала по оси вращения). Данные механических вибраций вызваны изменениями крутящего момента с течением времени, наложенными на постоянную скорость торсионного вала. В автомобилестроении основной причиной вибраций кручения становятся колебания полезной мощности двигателя.
Вибрации кручения оценивают как изменение скорости вращения в цикле вращения. Изменения частоты вращения обусловлены нестабильным крутящим моментом или переменной нагрузкой.
Что такое вибрация вращения?
Вибрация вращения — динамическая составляющая скорости вращения. При точном измерении вибрации вращения вала в некоторых участках разгона можно увидеть сильное отклонение скорости вращения. Отклонение возникает в результате угловой вибрации, пересекающей собственную угловую частоту вала. Угловая вибрация вычисляется путём отсечения постоянной составляющей скорости или угла вращения;
Отклонение возникает в результате угловой вибрации, пересекающей собственную угловую частоту вала. Угловая вибрация вычисляется путём отсечения постоянной составляющей скорости или угла вращения;
Вибрация кручения зависит от ряда параметров: свойств материала и условий эксплуатации (температуры, нагрузки, частоты вращения и т.д.).
Как измерять вибрацию вращения и кручения
В этом коротком видео показаны способы измерения вибрации и вращения, а также описана базовая теория и практические преимущества таких измерений.
Модуль вибрации кручения Dewesoft X автоматически вычисляет следующие параметры:
- угол поворота: фильтрованное значение угла вибрации;
- скорость вращения: фильтрованное значение скорости вибрации;
- угол кручения: динамический угол кручения, который представляет собой разность углов, полученных от датчика 1 и датчика 2;
- скорость кручения: разница угловых скоростей, полученных от датчика 1 и датчика 2;
- опорный угол по оси X: опорный угол, который всегда составляет от 0 до 360° и может быть использован в качестве опорного на графике XY;
- частота: об/мин.

Вычисления можно провести в ходе измерения, а также на этапе обработки (по необработанным данным).
Итог
Датчики крутящего момента применяются для решения сотен задач во всех отраслях. Датчики реактивного крутящего момента применяются в динамометрических ключах и других инструментах.
В автомобилестроении датчики крутящего момента устанавливают в стойки испытания двигателей, динамометры, испытательные стенды, а также стенды испытаний на долговечность. Но это лишь базовые применения, помимо которых датчики применяют для испытания промышленных установок кондиционирования воздуха, крупномасштабных кормушек для животных и птиц, робототехники, монтажного и медицинского оборудования, электрооборудования и т.д.
Крутящий момент — важный параметр в множестве отраслей. К счастью, его можно измерить с помощью датчиков и преобразователей, и отобразить, записать и проанализировать с помощью систем сбора данных.
Поделиться статьёй:
крутящий момент (2004) — IMDB
- Награды
- 4 Номинации
Videos2
Трейлер 2:31
Смотрейный крутящий момент
10109999999999911111101110.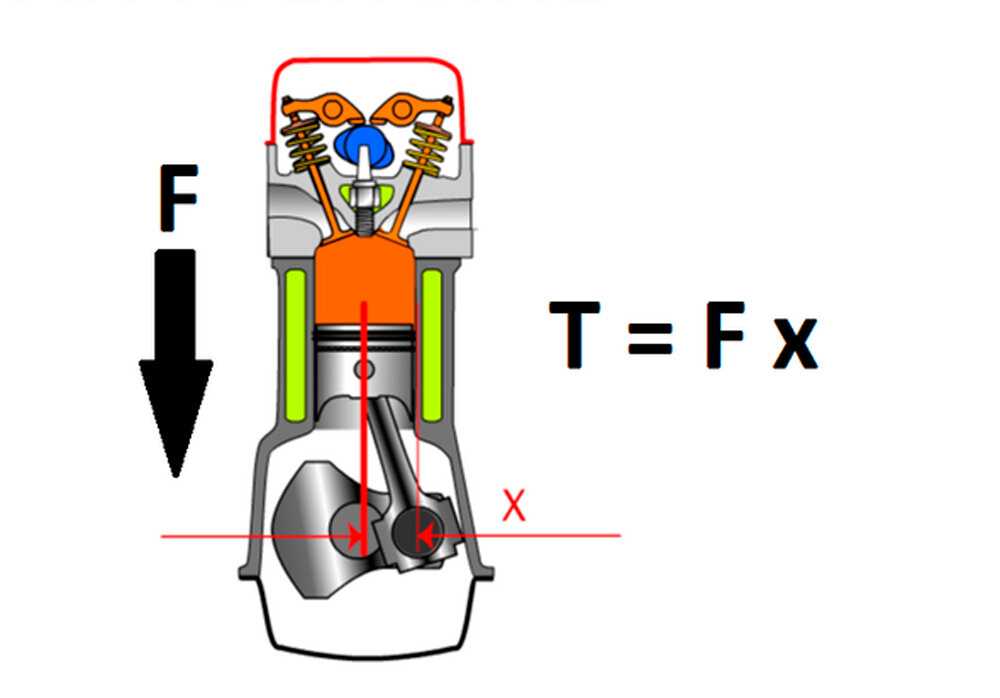 Photoers111111101110. Photoers111111101110. Photoers1111111011119. Photoern11111111111111113
Photoers111111101110. Photoers111111101110. Photoers1111111011119. Photoern11111111111111113
Мартин Хендерсон
Айс Кьюб
Моне Мазур
Джон Эшкер
- Водитель желтой машины
Макс Бизли
- Лютер 9 Кук
6
60013
- Neil Luff
John Doe
- Sheriff Barnes
Gichi Gamba
Lance Gilbert
- 18 Wheeler Driver
Jay Hernandez
- Dalton
Will Yun Lee
Faizon Love
Юстина Мачадо
- Хендерсон
Хейден МакФарланд
Кристина Милиан
Кинга Филипс
- Подруга Нила Лаффа
Jaime Pressly
Nichole Galicia
- Mikisha
- (as Nichole Mercedes Robinson)
- Joseph Kahn
- Matt Johnson
- All cast & crew
- Production, box офис и многое другое на IMDbPro
Еще нравится это
Biker Boyz
Следующий уровень
xXx
Torque
Cradle 2 the Grave
XXX: State of the Union
Born To Race
Автомобиль 19
Whirlygirl
XXX: возвращение ксандера клетки
Высоко Цитаты
Шейн: [Шейн и Форд едут на серийной гоночной машине] Форд, пробка!
Кэри Форд: Ой! Вот почему я ненавижу четыре колеса!
Отзывы пользователей228
Обзор
Избранный обзор
Примите это таким, какое оно есть, и, возможно, оно вам даже понравится!
Ну, я только что убил 81 минуту воскресного вечера на просмотр «Крутящего момента».
И мне понравилось!
Сцены погони становились все более нелепыми по ходу фильма, и, наконец, закончились компьютерной оргией, мало похожей на реальную жизнь (на самом деле это была чистая аркадная игра).
Сюжет также был довольно предсказуем, элементы сюжета и идеи были взяты из таких разных фильмов, как «Форсаж», «Трон» и «Воины», с добавлением всегда популярного «согнутого полицейского». также.
Но цыпочки были действительно ГОРЯЧИМИ, чуваки выглядели круто, Ice T был в своем насмешливом, рычащем изумительном виде, а саундтрек в стиле хэви-метал продвигал фильм вперед в отличном темпе.
Рейтинг 3.0 здесь не соответствует действительности, и, в целом, я бы сказал, что если вы не сядете и не посмотрите это, ожидая каких-либо высокоинтеллектуальных развлечений, и не будете наслаждаться красивыми девушками в обтягивающих байкерских костюмах и некоторые динамичные действия, вы не будете слишком разочарованы.
полезно•10
5
- Большой S-2
- 22 августа 2004 г.

Подробная информация
- Дата выпуска
- 16 января 2004 г. (США)
- Соединенные Штаты
- Соединенные Штаты
- .
- Английский
- , также известный как
- Bá Chủ ường đua
- 0223 Production companies
- Warner Bros.

- Village Roadshow Pictures
- Original Film
- Warner Bros.
- See more company credits at IMDbPro
- $40,000,000 (estimated)
- $21,215,059
- 9 970 557 $
- 18 января 2004 г.0010 Technical specs
1 hour 24 minutes
- DTS
- Dolby Digital
- SDDS
- 2.
 35 : 1
35 : 1
- 2.
Related news
Contribute to this page
Suggest отредактировать или добавить отсутствующий контент
Top Gap
Что такое схема сюжета на японском языке для Torque (2004)?
Ответ
10.6 Крутящий момент | Университетская физика Том 1
Цели обучения
К концу этого раздела вы сможете:
- Описывать, как величина крутящего момента зависит от величины плеча рычага и угла, который вектор силы образует с плечом рычага
- Определите знак (положительный или отрицательный) крутящего момента с помощью правила правой руки
- Рассчитайте отдельные крутящие моменты относительно общей оси и просуммируйте их, чтобы найти чистый крутящий момент
Важной величиной для описания динамики вращающегося твердого тела является крутящий момент. Мы видим применение крутящего момента во многих отношениях в нашем мире. У всех нас есть интуитивное представление о крутящем моменте, например, когда мы используем большой гаечный ключ, чтобы открутить упрямый болт.
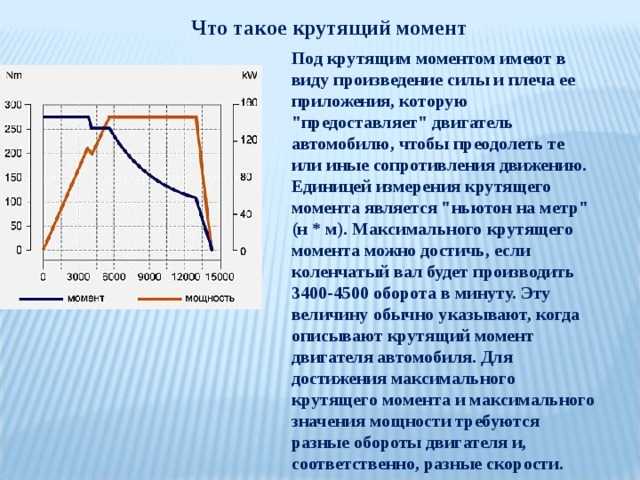
Определение крутящего момента
До сих пор мы определили множество переменных, которые являются вращательными эквивалентами своих поступательных аналогов. Рассмотрим, каким должен быть аналог силы. Поскольку силы изменяют поступательное движение объектов, вращательный аналог должен быть связан с изменением вращательного движения объекта вокруг оси. Мы называем этот вращательный аналог крутящим моментом .
В повседневной жизни мы постоянно вращаем объекты вокруг оси, поэтому интуитивно мы уже многое знаем о крутящем моменте.
 Рассмотрим, например, как мы поворачиваем дверь, чтобы открыть ее. Во-первых, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям; более эффективно повернуть дверь, если мы нажмем далеко от петель. Во-вторых, мы знаем, что толкать надо перпендикулярно плоскости двери; если мы нажмем параллельно плоскости двери, мы не сможем ее повернуть. В-третьих, чем больше сила, тем эффективнее она открывает дверь; чем сильнее вы нажимаете, тем быстрее открывается дверь. Первый пункт подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; второй подразумевает, что эффективность зависит от угла приложения силы; третий подразумевает, что величина силы также должна быть частью уравнения. Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота. (Рисунок) показывает вращение против часовой стрелки.
Рассмотрим, например, как мы поворачиваем дверь, чтобы открыть ее. Во-первых, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям; более эффективно повернуть дверь, если мы нажмем далеко от петель. Во-вторых, мы знаем, что толкать надо перпендикулярно плоскости двери; если мы нажмем параллельно плоскости двери, мы не сможем ее повернуть. В-третьих, чем больше сила, тем эффективнее она открывает дверь; чем сильнее вы нажимаете, тем быстрее открывается дверь. Первый пункт подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; второй подразумевает, что эффективность зависит от угла приложения силы; третий подразумевает, что величина силы также должна быть частью уравнения. Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота. (Рисунок) показывает вращение против часовой стрелки. 9{\text{′}} [/latex] действует на том же расстоянии r от шарниров. (c) Та же сила, что и в (a), создает меньший крутящий момент против часовой стрелки, когда она приложена на меньшем расстоянии от шарниров. (d) Меньший крутящий момент против часовой стрелки создается силой той же величины, что и (а), действующей на том же расстоянии, что и (а), но под углом [латекс] \тета [/латекс], который меньше, чем [латекс] 90\текст {°} [/латекс].
9{\text{′}} [/latex] действует на том же расстоянии r от шарниров. (c) Та же сила, что и в (a), создает меньший крутящий момент против часовой стрелки, когда она приложена на меньшем расстоянии от шарниров. (d) Меньший крутящий момент против часовой стрелки создается силой той же величины, что и (а), действующей на том же расстоянии, что и (а), но под углом [латекс] \тета [/латекс], который меньше, чем [латекс] 90\текст {°} [/латекс].Теперь рассмотрим, как определить крутящие моменты в общем трехмерном случае.
Крутящий момент
Когда сила [латекс] \overset{\to }{F} [/latex] приложена к точке P , положение которой равно [латекс] \overset{\to }{r} [/latex] относительно O ((Рисунок)), крутящий момент [латекс] \overset{\to }{\tau} [/latex] вокруг O составляет
[латекс] \overset{\to }{\tau} = \ overset {\ to {r} \, × \, \ overset {\ to {F}. [/latex]
Рис. /латекс], а его направление определяется по правилу правой руки.

Из определения векторного произведения крутящий момент [латекс] \overset{\to }{\tau} [/latex] перпендикулярен плоскости, содержащей [латекс] \overset{\to }{r}\,\ text{and}\,\overset{\to }{F} [/latex] и имеет величину
[латекс] |\overset{\to }{\tau}|=|\overset{\to }{r} \,×\,\overset{\to }{F}|=rF\text{sin}\,\theta , [/latex]
, где [latex] \theta [/latex] — угол между векторами [ латекс] \overset{\to }{r} [/латекс] и [латекс] \overset{\to }{F} [/латекс]. Единицей крутящего момента в СИ является ньютон, умноженный на метр, обычно записывается как [латекс] \текст{Н}·\текст{м} [/латекс]. Величина [латекс] {r}_{\perp}=r\text{sin}\,\theta[/latex] представляет собой перпендикулярное расстояние от O к линии, определяемой вектором [латекс] \overset{\to }{F} [/латекс] и называемой плечом рычага . Обратите внимание, что чем больше плечо рычага, тем больше величина крутящего момента. С точки зрения плеча рычага величина крутящего момента составляет
[латекс] |\overset{\to }{\tau}|={r}_{\perp}F.
 [/latex]
[/latex]Перекрестное произведение [латекс] \overset{\to }{r}\,×\,\overset{\to }{F} [/latex] также сообщает нам знак крутящего момента. На (рисунке) векторное произведение [латекс] \overset{\to }{r}\,×\,\overset{\to }{F} [/latex] расположено вдоль положительных z -ось, которая по соглашению является положительным крутящим моментом. Если [латекс] \overset{\to }{r}\,×\,\overset{\to }{F} [/latex] расположен вдоль отрицательной оси z , это создает отрицательный крутящий момент.
Если мы рассмотрим диск, который может свободно вращаться вокруг оси, проходящей через центр, как показано на (Рисунок), мы можем увидеть, как угол между радиусом [латекс] \overset{\to }{r} [/латекс ] и сила [латекс] \overset{\to }{F} [/латекс] влияет на величину крутящего момента. Если угол равен нулю, крутящий момент равен нулю; если угол [латекс] 90\text{°} [/latex], крутящий момент максимальный. Крутящий момент на (рис.) положительный, потому что направление крутящего момента по правилу правой руки выходит за пределы страницы вдоль положительной оси z .
 Диск вращается против часовой стрелки за счет крутящего момента в том же направлении, что и положительное угловое ускорение.
Диск вращается против часовой стрелки за счет крутящего момента в том же направлении, что и положительное угловое ускорение.Рис. 10.33 Диск может свободно вращаться вокруг своей оси, проходящей через центр. Величина крутящего момента на диске равна [латекс] rF\text{sin}\,\theta [/latex]. Когда [латекс] \theta =0\text{°} [/latex], крутящий момент равен нулю и диск не вращается. Когда [латекс] \ тета = 90\text{°} [/latex], крутящий момент максимальный и диск вращается с максимальным угловым ускорением.
Любое количество крутящих моментов может быть рассчитано относительно данной оси. Отдельные крутящие моменты складываются, чтобы создать чистый крутящий момент вокруг оси. Когда соответствующий знак (положительный или отрицательный) присваивается величинам отдельных крутящих моментов относительно указанной оси, чистый крутящий момент вокруг оси представляет собой сумму отдельных крутящих моментов:
[латекс] {\ overset {\ to } {\ тау }} _ {\ text {net}} = \ sum _ {i} | {\ overset {\ to } {\ tau}} _ {i} |.
 [/латекс]
[/латекс]Расчет чистого крутящего момента для твердых тел на неподвижной оси
В следующих примерах мы вычисляем крутящий момент как абстрактно, так и применительно к твердому телу.
Сначала мы представляем стратегию решения проблем.
Стратегия решения проблем: определение чистого крутящего момента
- Выберите систему координат с точкой вращения или осью вращения в качестве начала выбранной системы координат.
- Определите угол между плечом рычага [латекс] \overset{\to }{r} [/латекс] и вектором силы.
- Возьмите векторное произведение [латекс] \overset{\to }{r}\,\text{and}\,\overset{\to }{F} [/latex], чтобы определить, является ли крутящий момент положительным или отрицательным относительно точка вращения или ось.
- Оцените величину крутящего момента, используя [латекс] {r}_{\perp}F [/латекс].
- Присвойте величине соответствующий знак, положительный или отрицательный.
- Суммируйте крутящие моменты, чтобы найти чистый крутящий момент.

Пример
Расчет крутящего момента
Четыре силы показаны на (Рисунок) в определенных местах и ориентациях по отношению к данному xy -система координат. Найдите крутящий момент, вызванный каждой силой относительно начала координат, а затем используйте полученные результаты, чтобы найти чистый крутящий момент вокруг начала координат.
Рисунок 10.34 Четыре силы, создающие крутящий момент.
Стратегия
Эта задача требует расчета крутящего момента. Все известные величины — силы с направлениями и плечами рычага — приведены на рисунке. Цель состоит в том, чтобы найти каждый отдельный крутящий момент и чистый крутящий момент путем суммирования отдельных крутящих моментов. Будьте осторожны, чтобы присвоить правильный знак каждому крутящему моменту, используя векторное произведение [латекс] \overset{\to }{r} [/latex] и вектора силы [латекс] \overset{\to }{F} [/ латекс].
Решение
Используйте [латекс] |\overset{\to }{\tau}|={r}_{\perp }F=rF\text{sin}\,\theta [/latex] для нахождения величины и [латекс] \overset{\to }{\tau}=\overset{\to }{r}\,×\,\overset{\to }{F} [/latex] для определения знака крутящего момента.

Крутящий момент от силы 40 Н в первом квадранте определяется выражением [латекс] (4)(40)\text{sin}\,90\text{°}=160\,\text{N}·\text{ м} [/латекс].
Перекрестное произведение [латекс] \overset{\to }{r} [/latex] и [латекс] \overset{\to }{F} [/latex] находится за пределами страницы, положительно.
Крутящий момент от силы 20 Н в третьем квадранте определяется как [латекс] \text{−}(3)(20)\text{sin}\,90\text{°}=-60\,\text{ N}·\text{m} [/latex].
Перекрестное произведение [латекс] \overset{\to }{r} [/latex] и [латекс] \overset{\to }{F} [/latex] находится на странице, поэтому оно отрицательно.
Крутящий момент от силы 30 Н в третьем квадранте определяется формулой [латекс] (5)(30)\text{sin}\,53\text{°}=120\,\text{N}·\text{ м} [/латекс].
Перекрестное произведение [латекс] \overset{\to }{r} [/latex] и [латекс] \overset{\to }{F} [/latex] находится за пределами страницы, положительно.
Крутящий момент от силы 20 Н во втором квадранте определяется формулой [латекс] (1)(20)\text{sin}\,30\text{°}=10\,\text{N}·\text{ м} [/латекс].

Перекрестное произведение [латекс] \overset{\to }{r} [/latex] и [латекс] \overset{\to }{F} [/latex] отсутствует на странице.
Таким образом, чистый крутящий момент равен [латекс] {\tau}_{\text{net}}=\sum _{i}|{\tau}_{i}|=160-60+120+10=230\ ,\text{N}·\text{m}\text{.} [/latex]
Значение
Обратите внимание, что каждая сила, действующая в направлении против часовой стрелки, имеет положительный крутящий момент, тогда как каждая сила, действующая в направлении по часовой стрелке имеет отрицательный крутящий момент. Крутящий момент больше, когда расстояние, сила или перпендикулярные компоненты больше.
Пример
Расчет крутящего момента на твердом теле (рисунок) показывает несколько сил, действующих в разных местах и под разными углами на маховик. У нас есть [латекс] |{\overset{\to }{F}}_{1}|=20\,\text{N}, [/latex] [латекс] |{\overset{\to }{F} }_{2}|=30\,\text{N} [/латекс], [латекс] |{\overset{\to }{F}}_{3}|=30\,\text{N} [ /латекс] и [латекс] r=0,5\,\текст{м} [/латекс].
 Найдите чистый крутящий момент на маховике относительно оси, проходящей через центр.
Найдите чистый крутящий момент на маховике относительно оси, проходящей через центр.Рисунок 10.35 Три силы, действующие на маховик.
Стратегия
Мы рассчитываем каждый крутящий момент отдельно, используя перекрестное произведение, и определяем знак крутящего момента. Затем мы суммируем крутящие моменты, чтобы найти чистый крутящий момент.
Решение
Начнем с [латекс] {\overset{\to }{F}}_{1} [/латекс]. Если мы посмотрим на (рисунок), то увидим, что [латекс] {\overset{\to }{F}}_{1} [/латекс] образует угол [латекс] 90\текст{°}+60\текст {°} [/latex] с радиус-вектором [latex] \overset{\to }{r} [/latex]. Взяв векторное произведение, мы видим, что оно находится вне страницы и, следовательно, является положительным. Мы также видим это из расчета его величины:
[латекс] |{\overset{\to }{\tau}}_{1}|=r{F}_{1}\text{sin}\,150\text{°}=0,5\,\ текст{м}(20\,\текст{N})(0,5)=5,0\,\текст{N}·\текст{м}. [/latex]
Далее мы смотрим на [latex] {\overset{\to}}{F}}_{2} [/latex].
 Угол между [латекс] {\overset{\to }{F}}_{2} [/латекс] и [латекс] \overset{\to }{r} [/латекс] равен [латекс] 90\текст{ °} [/latex] и перекрестное произведение находится на странице, поэтому крутящий момент отрицательный. Его значение равно
Угол между [латекс] {\overset{\to }{F}}_{2} [/латекс] и [латекс] \overset{\to }{r} [/латекс] равен [латекс] 90\текст{ °} [/latex] и перекрестное произведение находится на странице, поэтому крутящий момент отрицательный. Его значение равно[латекс] |{\overset{\to }{\tau}}_{2}|=\text{−}r{F}_{2}\text{sin}\,90\text{°}=-0,5\,\text{m}(30\,\text{N})=-15,0\,\text{N}·\text{m}. [/latex]
Когда мы оцениваем крутящий момент из-за [латекса] {\overset{\to}}{F}}_{3} [/latex], мы видим, что угол, который он образует с [латексом] \overset{ \to }{r} [/latex] равен нулю, поэтому [латекс] \overset{\to }{r}\,×\,{\overset{\to }{F}}_{3}=0. [/latex] Следовательно, [латекс] {\overset{\to}}{F}}_{3} [/латекс] не создает никакого крутящего момента на маховике.
Оцениваем сумму крутящих моментов:
[латекс] {\tau }_{\text{net}}=\sum _{i}|{\tau }_{i}|=5-15=- 10\,\text{N}·\text{м}. [/латекс]
Значение
Ось вращения находится в центре масс маховика. Поскольку маховик находится на неподвижной оси, он не может свободно перемещаться.
 Если бы он находился на поверхности без трения и не был зафиксирован на месте, [латекс] {\ overset {\ to} {F}} _ {3} [/латекс] заставил бы маховик перемещаться, а также [латекс] {\ overset{\to}}{F}}_{1} [/latex]. Его движение было бы комбинацией поступательного движения и вращения.
Если бы он находился на поверхности без трения и не был зафиксирован на месте, [латекс] {\ overset {\ to} {F}} _ {3} [/латекс] заставил бы маховик перемещаться, а также [латекс] {\ overset{\to}}{F}}_{1} [/latex]. Его движение было бы комбинацией поступательного движения и вращения.Проверьте свое понимание
Большой океанский корабль сел на мель у береговой линии, как и судьба 9{5}\,\text{N} [/latex], действующий в точке . Для выравнивания корабля необходимо применить . Каков крутящий момент относительно точки контакта корабля с землей ((Рисунок))?
Рисунок 10.36 Судно садится на мель и наклоняется, что требует применения крутящего момента для возвращения судна в вертикальное положение.
Показать ответ
Резюме
- Величина крутящего момента относительно неподвижной оси рассчитывается путем нахождения плеча рычага в точке приложения силы и использования соотношения [латекс] |\overset{\to}{\tau }|= {r}_{\perp}F [/latex], где [latex] {r}_{\perp} [/latex] — расстояние по перпендикуляру от оси до линии, на которой лежит вектор силы.
- Знак крутящего момента находится по правилу правой руки. Если страница представляет собой плоскость, содержащую [латекс] \overset{\to }{r} [/latex] и [латекс] \overset{\to }{F} [/latex], тогда [латекс] \overset{\to {r}\,×\,\overset{\to }{F} [/latex] выходит за пределы страницы для положительных крутящих моментов и на страницу для отрицательных крутящих моментов.
- Чистый крутящий момент можно найти путем суммирования отдельных крутящих моментов относительно данной оси.
Концептуальные вопросы
Какие три фактора влияют на крутящий момент, создаваемый силой относительно определенной точки поворота?
Показать раствор
Приведите пример, в котором небольшая сила вызывает большой крутящий момент. Приведите другой пример, в котором большая сила действует на малый крутящий момент.
При уменьшении массы гоночного велосипеда наибольшая выгода достигается за счет уменьшения массы шин и колесных дисков.
 Почему это позволяет гонщику достичь большего ускорения, чем такое же уменьшение массы рамы велосипеда?
Почему это позволяет гонщику достичь большего ускорения, чем такое же уменьшение массы рамы велосипеда?Показать раствор
Может ли одна сила создать нулевой крутящий момент?
Может ли набор сил иметь чистый крутящий момент, равный нулю, и результирующую силу, отличную от нуля?
Показать раствор
Может ли набор сил иметь результирующую силу, равную нулю, и результирующий крутящий момент, отличный от нуля?
Показать раствор
Задачи
Два маховика незначительной массы и разных радиусов скреплены вместе и вращаются вокруг общей оси (см. ниже). Меньший маховик радиусом 30 см имеет шнур, на который действует тяговое усилие 50 Н. Какую тяговую силу нужно приложить к шнуру, соединяющему больший маховик радиусом 50 см, чтобы комбинация не вращалась?
Показать ответ
Болты с цилиндрической головкой на автомобиле затягиваются с моментом 62,0 Н[латекс] ·\text{м} [/латекс].
 Если механик использует ключ длиной 20 см, какую перпендикулярную силу он должен приложить к концу ключа, чтобы правильно затянуть болт?
Если механик использует ключ длиной 20 см, какую перпендикулярную силу он должен приложить к концу ключа, чтобы правильно затянуть болт?(а) Открывая дверь, вы толкаете ее перпендикулярно с силой 55,0 Н на расстоянии 0,850 м от петель. Какой крутящий момент вы прикладываете к петлям? (b) Имеет ли значение, если вы нажмете на той же высоте, что и петли? Есть только одна пара петель.
Показать раствор
При затяжке болта ключ нажимают перпендикулярно с усилием 165 Н на расстоянии 0,140 м от центра болта. Какой крутящий момент вы прилагаете в ньютон-метрах (относительно центра болта)?
Какой подвешенный груз необходимо поместить на шнур, чтобы шкив не вращался (см. следующий рисунок)? Масса на плоскости без трения равна 5,0 кг. Внутренний радиус шкива равен 20 см, а внешний радиус равен 30 см.
Показать ответ
Простой маятник состоит из невесомого троса длиной 50 см, соединенного со стержнем, и небольшого груза массой 1,0 кг, прикрепленного к другому концу.
Рассчитайте крутящий момент вокруг оси z , которая выходит за пределы страницы в начале координат на следующем рисунке, учитывая, что [латекс] {F}_{1}=3\,\text{N},\enspace {F}_{2}=2\,\text{N},\enspace{F}_{3}=3\,\text{N},\enspace{F}_{4}=1,8\,\ текст{N} [/латекс].
Показать ответ
Качели длиной 10,0 м и однородной массой 10,0 кг покоятся под углом [латекс] 30\text{°} [/латекс] к земле (см. следующий рисунок). Стержень расположен на высоте 6,0 м. Какую силу необходимо приложить перпендикулярно качелям на поднятом конце, чтобы качели едва начали вращаться?
Маятник состоит из стержня массой 1 кг и длиной 1 м, соединенного со стержнем, к другому концу которого прикреплена твердая сфера массой 0,5 кг и радиусом 30 см. Каков крутящий момент вокруг оси, когда маятник образует угол [латекс] 30\текст{°} [/латекс] по отношению к вертикали? 9{3}\text{N}·\text{m}\, [/latex] требуется, чтобы поднять разводной мост (см.

