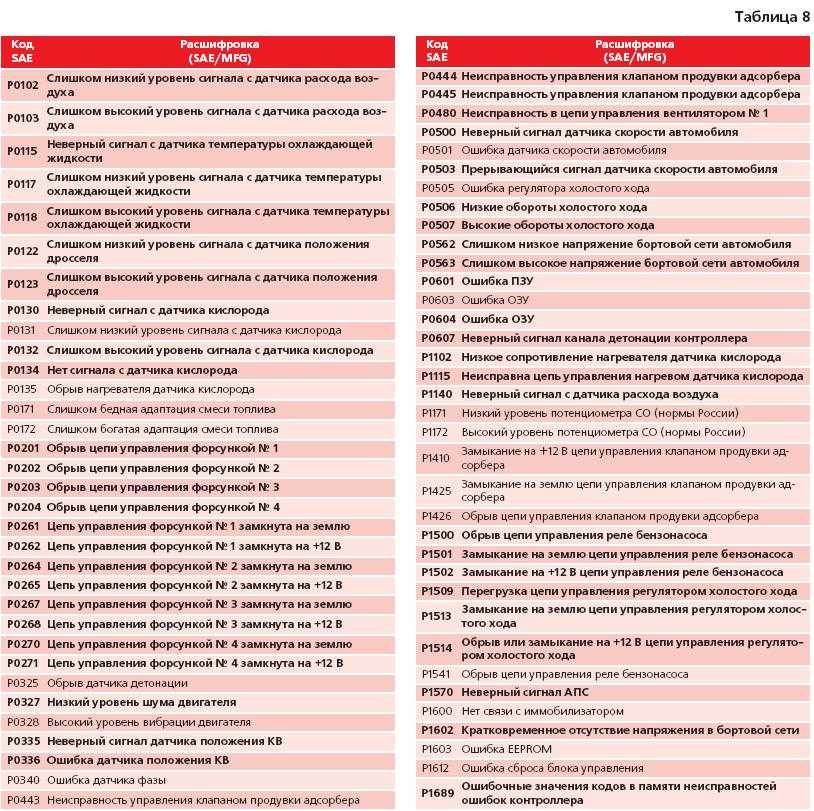
Расшифровка Ошибок Ваз 2115 Инжектор 8 Клапанов ~ AUTOTEXNIKA.RU
ВАЗ 2114 и 2115 коды ошибок. Простое дешифрование
Вам необходимо знать коды ошибок ВАЗ 2114 и 2115 для выполнения этой диагностики. Это облегчит поиск задачи. На самом деле, не зная расшифровки, не рекомендуется начинать диагностику. Когда вы лично получаете результат, например набор цифр, вы только почесываете голову, и проблема остается неизвестной.
Как правило, код ошибки похож на учебник, как контроллеры. Несколько аналогичных моделей могут быть оснащены однообразным крылом. Аналогичные контроллеры с 14-й и 15-й моделями также имеют ВАЗ 2113 и Самара-2.
Информация о контроллере доступна в технической документации вашего автомобиля. Вы также всегда найдете информацию об этом решении онлайн. Всегда обязательно найдите подробный список ошибок, прежде чем ставить диагноз.
Описанные выше ошибки не единственные. На практике существует много разных кодов:
- P0101-P0103 эти коды относятся к датчику расхода топлива.
- P0116-P0118. Неисправность датчика температуры антифриза. Может быть проблема с проводкой, так как лучше сначала проверить цепь питания датчика;
- P0112-P0113 Этот код появляется, когда датчик показывает температуру воздуха на впуске. Часто появляется с небольшой цепью в проводке;
- Ряд ошибок (P2122, P2138, P222, P2123, P223) сообщают о дилеммах с контролем положения акселератора;
- P0130-P0134. Датчик кислорода для консистенции должен быть заменен. Перед этим проверьте состояние проводки, которая питает датчик;
- P0201-P0204. препятствия с насадками. Замок, скорее всего, называется замком. Обязательно проверьте провода, которые их питают;
- P0136-P0140, такие коды указывают на неисправность датчиков, контролирующих образование консистенции в системе впрыска;
- P0326-P0328. поломка детонации устройства. Это может иногда появляться, когда отказывает блок управления двигателем;
- P0351-P0352, P2301, P2304 такие показания указывают на неисправность катушек зажигания, как правило, с этими ошибками запускается двигатель;
- P0691-P0692.
выход из строя первого реле вентилятора, работающего в системе охлаждения; - P0485. неправильный сигнал напряжения от охлаждающего вентилятора;
- P0693-P0694, Произошел сбой второго охлаждающего реле, которое позволяет вести учет (программное обеспечение). В таком случае вскипятите антифриз и перегрейте двигатель. Чтобы избежать более сложной поломки, проблема должна быть устранена;
- P0422 неисправность преобразователя, требуется замена узла;
- P0560-P0563. нарушено напряжение в бортовой сети, проверено состояние аккумулятора;
- P0627-P0629. Неверный сигнал от датчика топливного насоса. Если все это запускает двигатель, значит, проблема в датчике. Отказ самого бензонасоса делает невозможным запуск двигателя.
Клапан инжектора ВАЗ 2115 Объяснение 8.
Диагностика ЭБУ ВАЗ Коды ошибок
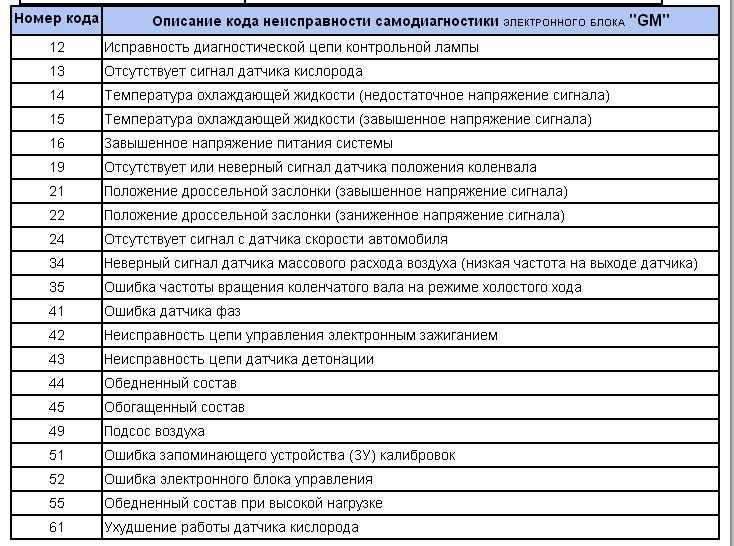
Самодиагностика электрических систем для автомобилей десятого семейства ВАЗ. Отображается на приборной панели.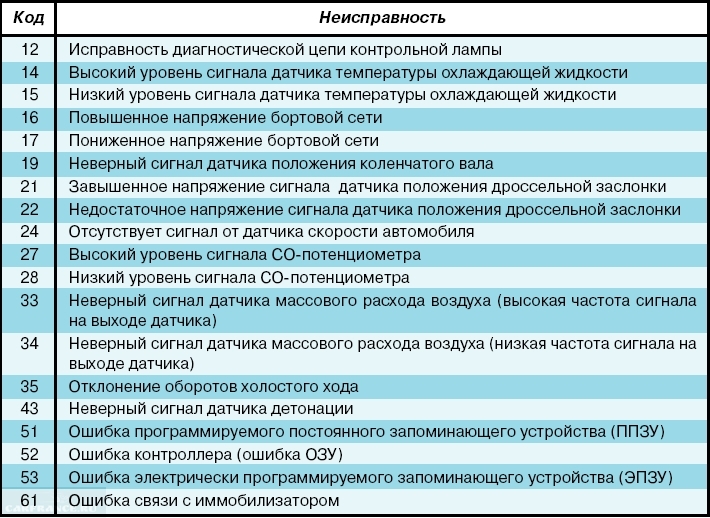
Это самые основные коды ошибок. Дополнительную информацию можно найти в файле, обычно в комплекте с диагностической программой. Все найденные неисправности должны быть устранены. Затем ошибка сбрасывается и выполняется повторная проверка.
Если под рукой нет сканера или ноутбука, вы можете выполнить мини-диагностику. Для этого зажмите кнопку одометра (расположена на приборной панели). При этом зажигание включено. Затем кнопка отпущена. Стрелки устройств начинают прыгать. Затем он нажимается один раз на одометр. Номер прошивки будет отображаться. Нажмите и отпустите кнопку еще раз.
Таким образом, вы можете увидеть двузначный код ошибки. Однако следует отметить, что не все неисправности могут быть диагностированы таким образом. Следовательно, это не заменит полный диагноз.
Вывод. Проблемы с управлением двигателем не редкость. Поэтому способность самостоятельно диагностировать проблемы не будет лишней. Для этого вам необходимо знать коды ошибок ВАЗ 2114 и 2115.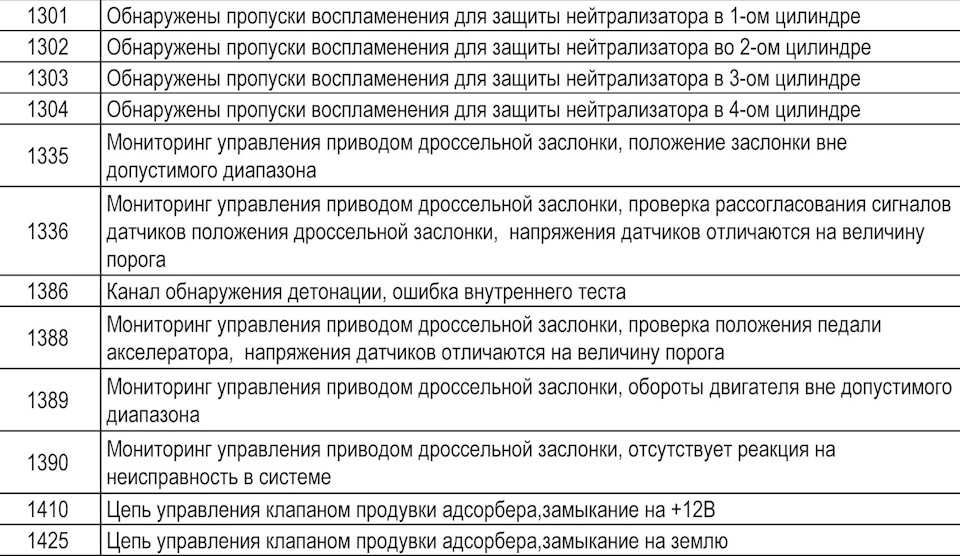
Вам также понадобится сканер или ноутбук с установленной программой. Обычно это оборудование простое в использовании.
Коды ошибок Ваз 2115, инжектор 8 клапанов.
Источник
M5410 Теория кодирования 1
M5410 Теория кодирования 1 Теория кодирования возникла с появлением компьютеров. Ранние компьютеры были огромными механических монстров, надежность которых была низкой по сравнению с сегодняшними компьютерами. Основанный на, как они были, на банках механических реле, если одно реле не могло замкнуть весь расчет был ошибочным. Инженеры того времени разработали способы обнаружения неисправных реле, чтобы их можно было заменить. Пока Р. У. Хэмминг работал в Bell Labs, из-за разочарования с бегемотом, с которым он работал, пришла в голову мысль, что если машина способный понять, что он ошибся, разве машина не может исправить это ошибка. Принявшись за работу над этой проблемой, Хэмминг разработал способ кодирования информации. что, если ошибка была обнаружена, ее также можно было исправить.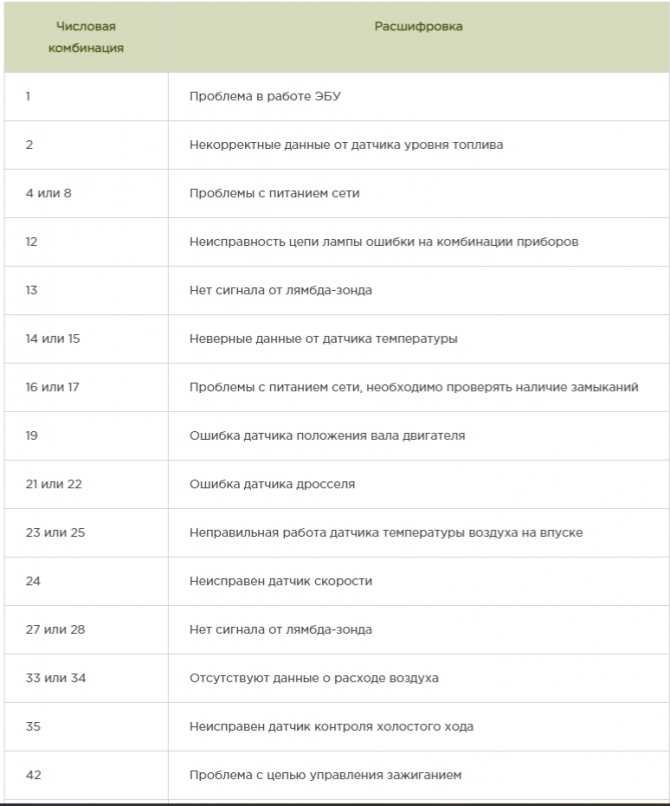
То, что мы назвали теорией кодирования, правильнее было бы назвать теорией кодирования. Коды, исправляющие ошибки, поскольку есть еще один аспект теории кодирования, более старый и занимается созданием и расшифровкой секретных сообщений. Эта область называется криптографией и нам это будет неинтересно. Скорее, проблема, которую мы хотим решить, связана с трудности, связанные с передачей сообщений. В частности, предположим, что мы хотел передать сообщение и знал, что в процессе передачи будет некоторое изменение сообщения из-за слабых сигналов, спорадических электрических всплесков и других естественный шум, проникающий в среду передачи. Проблема в том, чтобы застраховать что предполагаемое сообщение может быть получено из того, что фактически получено. Один простой Подход к этой проблеме заключается в том, что называется повторяющимся кодом. Например, если мы хотим отправить сообщение ПЛОХИЕ НОВОСТИ, мы могли повторять каждую букву определенное количество раз и отправлять, скажем,
BBBBAAAAADDDDD NNNNNEEEEEWWWWWSSSSS.Даже если несколько эти письма искажались при передаче, предполагаемое сообщение можно было восстановить из получено сообщение, которое может выглядеть как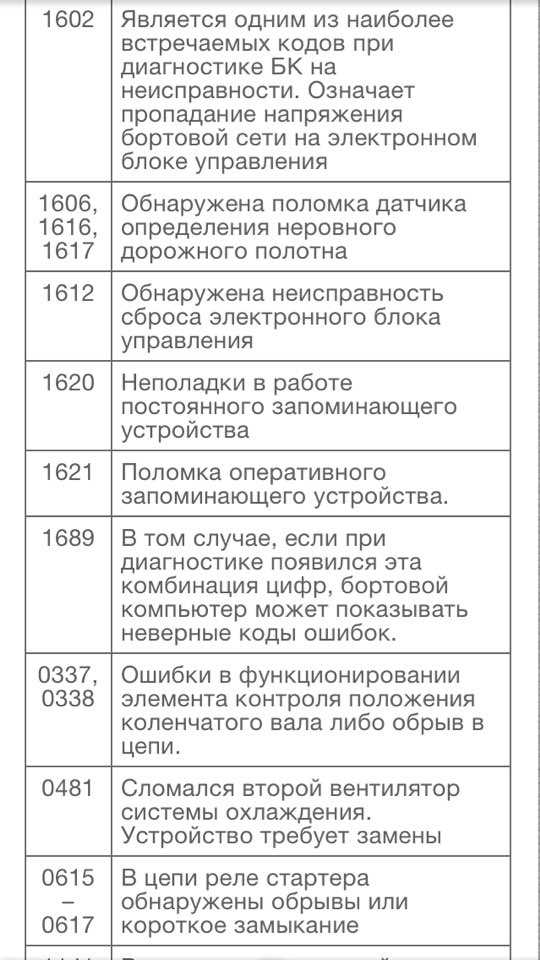
процессом, называемым мажоритарным декодированием , что в данном случае означало бы, что для каждого блока из 5 букв предполагаемой буквой является та, которая чаще всего встречается в блоке. блокировать. Проблема этого подхода в экономике, повторяющийся код не очень эффективен. увеличение длины передаваемого кода и, следовательно, увеличение времени и энергии, необходимых для передать его, необходимо для того, чтобы иметь возможность правильно декодировать сообщение, но как эффективное использование этого увеличения в процедуре кодирования зависит от схемы кодирования. Предполагать, в нашем примере вероятность того, что буква будет искажена при передаче, равна p = 0,05 и, следовательно, д = 1 — р = 0,95 — вероятность того, что письмо будет получено правильно. Без какого-либо кодирования, Вероятность того, что наше сообщение из 8 букв (включая пробелы) будет правильно принято, равна q 8 = 0,66.BBBEBFAAAADGDDD. MNNNTEEEEEWWWSWRRSSS,
При использовании повторяющегося кода вероятность правильного декодирования данной буквы равна q 5 + 5q 4 p +
10q 3 p 2 = 0,9988, поэтому вероятность получения правильного сообщения после декодирования равна
(0,9988) 8 = 0,990, явное увеличение по сравнению с незакодированным сообщением, но это 1%
вероятность получения неправильного сообщения может быть неприемлемой для некоторых приложений. К
увеличить вероятность декодирования правильного сообщения с помощью этого типа кода, мы бы
необходимо увеличить количество повторений — исправление, которое может быть нежелательным или даже невозможным в
определенные ситуации. Однако, как мы увидим, другие схемы кодирования могут увеличить
вероятность до 0,9999 без увеличения длины закодированного сообщения. Прежде чем оставить повторяющиеся коды и перейти к другим схемам кодирования, давайте представим некоторые терминология. Каждый блок повторяющихся символов называется кодовым словом
е. кодовым словом является то, что
передается вместо одной части информации в исходном сообщении. Набор всего кода
слов называется кодом . Если все кодовые слова в коде имеют одинаковую длину, то код
называется блок-кодом . Повторяющиеся коды являются блочными кодами. Одна функция, которую должен иметь полезный код
есть способность обнаруживать ошибки. Повторяющийся код с кодовыми словами длиной 5 может
всегда обнаруживают от 1 до 4 ошибок, допущенных при передаче кодового слова, так как любые 5 букв
слово, состоящее более чем из одной буквы, не является кодовым словом. Однако можно на 5
ошибки остаются незамеченными (как?). Мы бы сказали, что этот код равен 9.0008 4-обнаружение ошибки
. Другой
особенностью является способность исправлять ошибки, т. е. способность декодировать правильную информацию из
ошибка, пронизанная полученными словами. Повторяющийся код, с которым мы имеем дело, всегда может исправить 1 или
2 ошибки, но может неправильно декодировать слово с 3 или более ошибками, поэтому это 2-ошибка
код исправления .
ОСНОВНЫЕ И ЛИНЕЙНЫЕ КОДЫ
Предположим, вы знали, что было передано английское слово, и вы получили слово КОРАБЛЬ. Если вы подозреваете, что при передаче произошли какие-то ошибки, невозможно определить, какое слово действительно передавалось — это могли быть ПРОПУСК, МАГАЗИН, СТОП, ЭТО, на самом деле любое слово из четырех букв. Проблема здесь в том, что английские слова находятся в смысл «слишком близко» друг к другу. Что придает коду способность исправлять ошибки, так это тот факт, что кодовые слова находятся «далеко друг от друга». Через мгновение мы уточним эту идею расстояния.
Мы беспокоимся
затем с двоичными блочными кодами. Слова (кодовые и другие), с которыми мы имеем дело
Таким образом, это упорядоченные n-кортежи из 0 и 1, где n — длина слов. Это может быть
абстрактно рассматриваемые как элементы n-мерного векторного пространства над полем GF(2). Расстояние Хэмминга между двумя словами — это количество мест, в которых они различаются. Так, например, слова (0,0,1,1,1,0) и (1,0,1,1,0,0) будут иметь расстояние Хэмминга 2. Это расстояние Хэмминга является метрикой векторного пространства, т. е. если d(x,y) обозначает расстояние Хэмминга расстояние между векторами x и y, то d удовлетворяет:
- д(х,х) = 0
- d(x,y) = d(y,x), и
- d(x,y) + d(y,z) >= d(x,z)
Минимальное расстояние кода C — это наименьшее расстояние между любой парой различных
кодовые слова в C (при условии, что C конечно).
Это минимальное расстояние кода, которое
измеряет возможности кода по исправлению ошибок. Если минимальное расстояние кода C равно 2e +
1, то C является кодом с исправлением ошибок e, поскольку, если в кодовом слове допущено e или меньше ошибок,
полученное слово ближе к исходному кодовому слову, чем к любому другому кодовому слову, и поэтому
можно правильно расшифровать.
Вес слова — это количество ненулевых компонентов в векторе. Альтернативно, вес — это расстояние слова от нулевого вектора. Изучение весов кодовые слова иногда дают полезную информацию о конкретном коде.
Важным классом кодов являются линейные коды , это те коды, код которых слова образуют подвекторное пространство. Если векторное пространство всех слов n-мерно и подпространство является k-мерным, тогда мы говорим о подпространстве как о (n,k)-линейном коде.
В общем, нахождение минимального расстояния кода требует сравнения каждой пары
отдельные элементы. Однако для линейного кода в этом нет необходимости.
Предложение VI.1.1 — В линейном коде минимальное расстояние равно минимальному весу среди всех ненулевых кодовых слов .
Доказательство: Пусть x и y — кодовые слова в коде C, тогда x — y находится в C, так как C линейный. Мы тогда имеют d(x,y) = d(x-y,0), что является весом x-y.
Теперь мы рассмотрим два способа описания линейного кода C. Первый задается
порождающая матрица G, строками которой является набор базисных векторов линейного подпространства C.
Поскольку свойство, которое нас больше всего интересует, — это возможное исправление ошибок, и это свойство
не изменится, если во всех кодовых словах поменять местами два символа (например, первую и вторую букву
каждого кодового слова) мы будем называть два кода эквивалентными, если один из них можно получить, применяя
фиксированная перестановка символов на слова другого кода. Имея это в виду, мы видим, что
для каждого линейного кода существует эквивалентный код, который имеет порождающую матрицу вида G
= [I k P], где I k — единичная матрица k на k, а P — матрица k на n-k.
Мы называем это
стандартная форма G .
Теперь мы подошли ко второму описанию линейного кода C. Ортогональное дополнение из C, т. е. множество всех векторов, ортогональных каждому вектору в C [ортогональный = внутренний произведение равно 0], является подпространством и, следовательно, другим кодом, называемым -двойным кодом языка C, и обозначаемым С’. Если H является порождающей матрицей для C’, то H называется проверка четности матрица для C. В общем проверкой четности для кода C является вектор x, который ортогонален всем кодовым словам C, и мы будет называть любую матрицу H матрицей проверки на четность, если строки H порождают двойственный код C. Следовательно, код C определяется такой проверочной матрицей H следующим образом:
С знак равно { Икс | хН т = 0 }.
Рассмотрим пример. Пусть C будет (7,4)-линейным кодом, порожденным строками G:
1 0 0 0 1 1 0
G = 0 1 0 0 0 1 1
0 0 1 0 1 1 1
0 0 0 1 1 0 1
Мы получаем 16 кодовых слов, умножая G слева на 16 различных векторов-столбцов
длина 4 над GF(2).
Они есть:
0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 1 1 0 1 0 0 0 0 1 1 0 1 0 0 0 0 1 1 0 1 1 0 0 0 1 1 0 0 1 0 0 0 1 1 1 0 1 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 1 1 1 1 0 0 1 0 1 1 1 1 0 0 1 0 1 1 1 1 0 0 1 0 0 1 1 1 0 0 1 1 0 1 1 1 0 0 0 1 0 1 1 1 0Обратите внимание, что имеется 7 кодовых слов веса 3, 7 веса 4, 1 веса 7 и 1 веса. 0. Поскольку это линейный код, минимальное расстояние этого кода равно 3, поэтому это 1-ошибка. корректирующий код.
Матрица проверки на четность для этого кода имеет вид
1 0 1 1 1 0 0
Н = 1 1 1 0 0 1 0
0 1 1 1 0 0 1
[Подтвердите это]. Этот код широко известен как (7,4)-код Хэмминга , являющийся одним из серии линейных кодов. коды Хэмминга и Голея.
КОДЫ АДАМАРА И МОРСКАЯ 9 МИССИЯ
Пусть H — матрица Адамара порядка 4m. Возьмите строки H и строки -H и измените все записи -1 на 0. Это дает нам 8m векторов длины 4m над полем GF(2). Сейчас по свойства матриц Адамара расстояние между любыми двумя различными векторами либо 2м или 4м.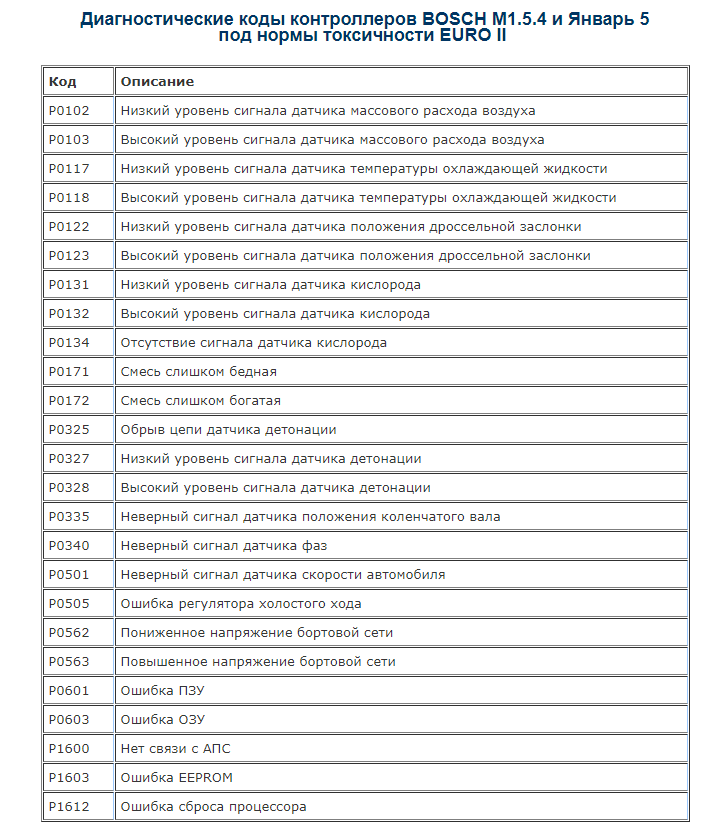
[Подтвердить] Таким образом, если рассматривать эти строки как код, минимальное расстояние равно
2m и код будет (m-1)-исправлением ошибок. Образованные таким образом коды называются
Коды Адамара или, если матрица Адамара образована прямым произведением порядка
2 Матрица Адамара, Коды Рида-Маллера первого рода .
Для изучения процесса использования кодов рассмотрим реальное приложение. Моряк 9
был космическим зондом, задачей которого было пролететь мимо Марса и передать изображения обратно на Землю.
черно-белая камера на борту «Маринера-9» сделала снимки, а затем появилась мелкая сетка.
размещают над картинкой и для каждого квадрата сетки измеряют степень черноты на
шкала от 0 до 63. Эти числа, выраженные в двоичном формате, представляют собой данные, которые передаются в
Земли (точнее в Лабораторию реактивного движения Калифорнийского института
технологии в Пасадене). По прибытии сигнал очень слабый и его необходимо усилить. Шум
от пространства, добавляемого к сигналу, и тепловые шумы от усилителя имеют эффект, что он
иногда случается, что сигнал, переданный как 1, интерпретируется приемником как 0 и
наоборот.
Если вероятность того, что это произойдет, равна 0,05, то по расчетам, выполненным в
Введение, если бы не было кодирования, примерно 26% полученного изображения было бы
неправильно. Таким образом, очевидно, что необходимо закодировать эту информацию кодом, исправляющим ошибки.
Теперь вопрос в том, какой код следует использовать? Любой код увеличит размер данных
отправляются, и это создает проблему. Моряк 9является небольшим транспортным средством и не может перевозить
огромный передатчик, поэтому передаваемый сигнал должен был быть направленным, но на большие расстояния
связанный с направленным сигналом имеет проблемы с выравниванием. Таким образом, существовал максимальный размер того, как
за один раз можно было передать много данных (пока передатчик был выровнен). Это оказалось
примерно в 5 раз больше исходных данных, поэтому, поскольку данные состояли из 6 бит (0,1
— векторы длины 6) кодовые слова могут иметь длину около 30 бит. Пятикратный код был
возможность, имеющая то преимущество, что ее очень легко реализовать, но это всего лишь 2 ошибки
исправление.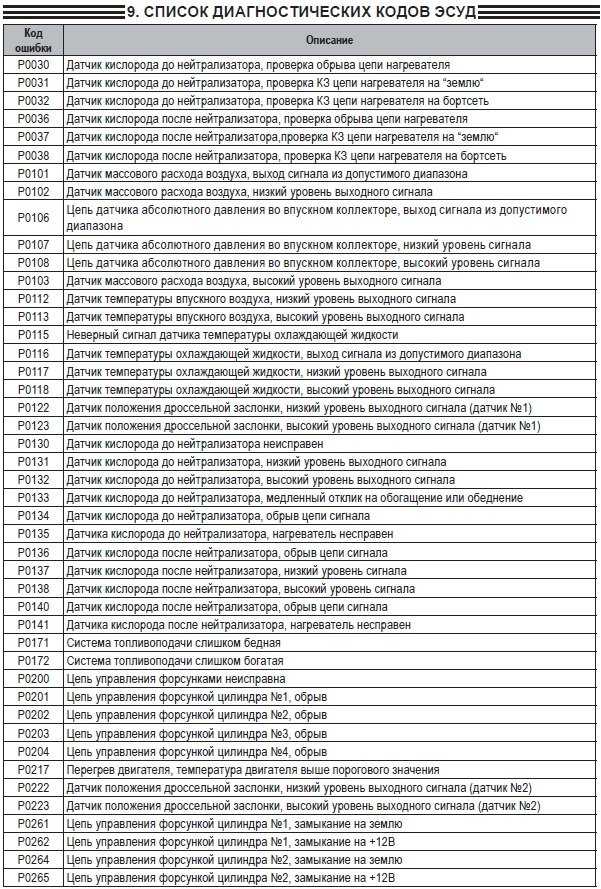
С другой стороны, код Адамара, основанный на матрице Адамара порядка 32.
будет исправлять 7 ошибок, и поэтому стоит дополнительных трудностей с его реализацией. Используя это
код, вероятность ошибки в изображении снижается всего до 0,01% (5-кратный код будет
имеют вероятность ошибки около 1%).
Обратимся теперь к проблемам кодирования и декодирования с помощью алгоритма Адамара.
код. На первый взгляд, кодирование не представляет проблемы, ведь существует 64 типа данных.
и 64 кодовых слова — поэтому любое произвольное присвоение типа данных кодовому слову будет работать.
проблема заключается в том, что Mariner 9 мал, и такой подход потребовал бы хранения
все 64 32-битных кодовых слова. Получается экономичнее, по площади и весу,
разработать аппаратное обеспечение, которое будет фактически вычислять кодовые слова, а не считывать их из
сохраненный массив. При правильном выборе матрицы Адамара код Адамара примет вид
быть линейным кодом, и поэтому этот расчет просто умножает данные на порождающую матрицу
кода.
Правильный выбор матрицы Адамара — это тот, который получен многократно
взятие прямого произведения матрицы Адамара порядка 2. [Докажите, что такой код Адамара
линейна по индукции].
Теперь рассмотрим проблему декодирования. Простая схема декодирования выглядит следующим образом:
полученный сигнал, т. е. последовательность из 32 нулей и единиц, сначала преобразуется в форму ±1 (путем
меняя каждый 0 на -1). Если результатом является вектор x и ошибок нет, то xHt, где
H — исходная матрица Адамара, будет вектором с 31 компонентой, равной 0 и единице
составляющая равна либо ±32. При наличии ошибок эти номера изменяются, но если
количество ошибок не более 7, то значения 0 могут увеличиться не более чем до 14, а значение
32 может уменьшиться не менее чем до 18. Таким образом, максимальная запись в xH t скажет нам, какой ряд
H или -H (если он отрицательный). Хотя это фактический алгоритм, используемый для декодирования
сигналов Mariner 9, он немного медленный с вычислительной точки зрения (требуется 322
умножения и соответствующие добавления для каждого кодового слова), поэтому ряд
используются вычислительные приемы, чтобы сократить фактическое вычисление до менее чем 1/3 того, что
требует алгоритм.
ССЫЛКИ
Существует много текстов, посвященных теории кодирования, некоторые из которых имеют особое значение:ER Berlekamp, Алгебраическая теория кодирования , McGraw-Hill, NY 1968.
ЕСЛИ. Блейк и Р.К. Маллин, Введение в алгебраическую и комбинаторную теорию кодирования , Academic Press, Нью-Йорк, 1976.
П.Дж. Кэмерон и Дж.Х. Ван Линт, Теория графов, теория кодирования и блочные конструкции , Издательство Кембриджского университета, Кембридж, 1975.
В.В. Петерсон и Э.Дж. Уэлдон-младший, Коды исправления ошибок , MIT Press, Кембридж, 1972.
В. Плесс, Введение в теорию кодов, исправляющих ошибки , Wiley, Нью-Йорк, 1982.
Ф.Дж. МакВильямс и Н.Дж.А. Слоан, Теория кодов, исправляющих ошибки , Северная Голландия, Амстердам, 1977 г.
Миссия Mariner 9 и теория кодирования, использованная в этом проекте, являются предметом
Дж.